题目内容
如图,矩形ABCD的对角线AC、BD相交于点O,DE∥AC,CE∥BD.
(1)判断四边形OCED的形状,并进行证明;
(2)点E是否在AB的垂直平分线上?若在,请进行证明;若不在,请说明理由.

证明:(1)证明:∵DE∥AC,CE∥BD,
∴四边形DOCE是平行四边形,
∵矩形ABCD的对角线AC、BD相交于点O,
∴AO=CO=DO=BO,
∴平行四边形OCED为菱形;
(2)解:AE=BE
理由:连接AE,BE
∵四边形OCED为菱形,
∴ED=CE,∴∠EDC=∠ECD,
∴∠ADE=∠BCE,
在△ADE和△BCE中,

∴△ADE≌△BCE(SAS),
∴AE=BE.
∴点E在AB的垂直平分线上

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的周长为
的周长为 ,且
,且 ,又
,又 ,D为垂足,
,D为垂足, 的周长为
的周长为 ,那么AD的长为( ).
,那么AD的长为( ). B.
B. C.
C. D.
D.

 ×[-32×(-
×[-32×(- )2+(-2)3]
)2+(-2)3] ,则袋中红球约为 _____个.
,则袋中红球约为 _____个. 与x轴的两个交点坐标.
与x轴的两个交点坐标.  D.6
D.6 角,那么cosα的值等于( )
角,那么cosα的值等于( )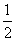 B.
B. C.
C.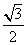 D.1
D.1