题目内容
6.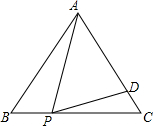 如图,正△ABC中,P为BC上一点,D为AC上一点,∠APD=60°,BP=1,CD=$\frac{2}{3}$,则△ABC的边长为3.
如图,正△ABC中,P为BC上一点,D为AC上一点,∠APD=60°,BP=1,CD=$\frac{2}{3}$,则△ABC的边长为3.
分析 根据题意可得:设△ABC的边长为x,根据等边三角形的性质得到∠DCP=∠PBA=60°.根据已知条件得到∠BAP=∠CPD.推出△ABP∽△CPD.由相似三角形的性质得到$\frac{BP}{CD}=\frac{AB}{PC}$,代入数据即可得到结论.
解答 解:设△ABC的边长为x,
∵△ABC是等边三角形,
∴∠DCP=∠PBA=60°.
∵∠APC=∠APD+∠DPC=∠BAP+∠ABP,∠APD=60°,
∴∠BAP=∠CPD.
∴△ABP∽△CPD.
∴$\frac{BP}{CD}=\frac{AB}{PC}$,
∴$\frac{1}{\frac{2}{3}}$=$\frac{x}{x-1}$.
∴x=3.
即△ABC的边长为3.
故答案为:3.
点评 本题考查了相似三角形的判定和性质,等边三角形的性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
17.下列计算结果正确的是( )
| A. | -3-2=-5 | B. | -|2|=2 | C. | 1÷(-3)=$\frac{1}{3}$ | D. | -2×3=6 |
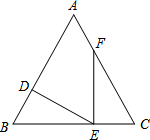 在△ABC中,AB=AC=5,BC=6,点D在边AB上,DE⊥AB,点E在边BC,点F在边AC上,且∠DEF=∠B.
在△ABC中,AB=AC=5,BC=6,点D在边AB上,DE⊥AB,点E在边BC,点F在边AC上,且∠DEF=∠B.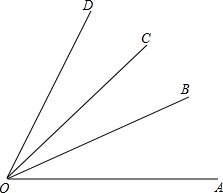 如图,OB、OC把∠AOD平分成三个相等的角,则OB是∠AOC的平分线,OC是∠BOD平分线.若OM是∠BOC的平分线,则OM也是∠AOD的平分线.
如图,OB、OC把∠AOD平分成三个相等的角,则OB是∠AOC的平分线,OC是∠BOD平分线.若OM是∠BOC的平分线,则OM也是∠AOD的平分线. 如图所示,
如图所示,