题目内容
 如图,四边形OABC是平行四边形,它具有对边相等的性质,即OA=BC,AB=OC,AB交y轴于点E,∠AOE=30°,OA=2
如图,四边形OABC是平行四边形,它具有对边相等的性质,即OA=BC,AB=OC,AB交y轴于点E,∠AOE=30°,OA=2| 3 |
| 3 |
(1)求点E,B的坐标;
(2)求平行四边形OABC的周长.
分析:(1)由∠AOE=30°,∠AEO=90°,即可求得AE的长,继而求得BE的长,则可求得点E,B的坐标;
(2)由(1),即可得AB=OC=5
,OA=BC=2
,继而求得平行四边形OABC的周长.
(2)由(1),即可得AB=OC=5
| 3 |
| 3 |
解答:解:(1)∵∠AOE=30°,∠AEO=90°,
∴AE=
OA=
×2
=
,
∵AB=0C=5
,
∴BE=AB-AE=4
,
∵OE=3,
∴A(-
,3),B(4
,3);
(2)平行四边形OABC的周长为:OA+AB+BC+OC=5
+5
+2
+2
=14
.
∴AE=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
∵AB=0C=5
| 3 |
∴BE=AB-AE=4
| 3 |
∵OE=3,
∴A(-
| 3 |
| 3 |
(2)平行四边形OABC的周长为:OA+AB+BC+OC=5
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
点评:此题考查了平行四边形的性质与含30°直角三角形的性质.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
 动.过点N作NP⊥OA于点P,连接AC交NP于Q,连接MQ.
动.过点N作NP⊥OA于点P,连接AC交NP于Q,连接MQ.  在MN上,并与MN上的点G重合,折痕为EF,点F为折痕与y轴的交点.
在MN上,并与MN上的点G重合,折痕为EF,点F为折痕与y轴的交点.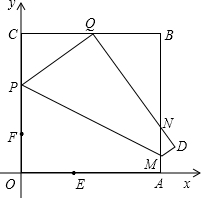
 (2012•呼伦贝尔)如图,四边形OABC是边长为2的正方形,反比例函数
(2012•呼伦贝尔)如图,四边形OABC是边长为2的正方形,反比例函数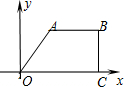 是( )
是( )