题目内容
能够成为直角三角形三条边长的三个正整数,我们称之为勾股数,观察下列表格所给的三个数a,b,c,a<b<c.

(1)试找出它们的共同点,并证明你的结论;
(2)写出当a=17时,b,c的值.
(1)这些勾股数的共同特点是:①以上各组数均满足a2+b 2=c2;②最小数(a)32=9=4+5,52=25=12+13,72=49=24+25,…
2=c2;②最小数(a)32=9=4+5,52=25=12+13,72=49=24+25,…
由以上特点,我们可以猜想这样一个结论:设m是大于1的奇数,将m2拆分为两个连续的整数之和,即m2=n+(n+1),则m,n,n+1就构成一组勾股数.
证明:∵ m2=n+(n+1),∴ m2+n2=2n+1+n2=(n+1)2.根据勾股定理的逆定理,m,n,n+1能够成为直角三角形的三边长.∴ m,n,n+1是一组勾股数.
(2)运用上面得出的结论,当a=17时,∵ 172=289=144+145,∴ b=144,c=145.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
 BC于D,那么图中的全等三角形共有 _________ 对.
BC于D,那么图中的全等三角形共有 _________ 对.
 ÷
÷ .
.
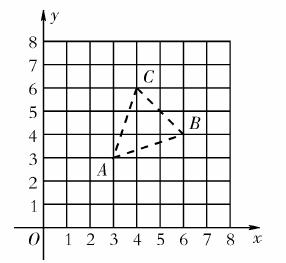
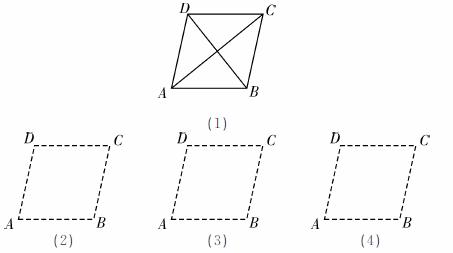
 完全相同的方格纸,方格纸中的每个小正方形的边长均为
完全相同的方格纸,方格纸中的每个小正方形的边长均为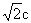 ,面积为6的等腰三角形.
,面积为6的等腰三角形.
 ,x1•x2=
,x1•x2= .
. +
+ 的值为
的值为