Question

周长为有理数的等腰三角形，底边上的高是底边长的，则该三角形的

1. A.
   腰和底边的高都是有理数
2. B.
   腰和底边的高都不是有理数
3. C.
   腰是有理数，底边上的高是无理数
4. D.
   腰是无理数，底边上的高是有理数

Answer 1

A
分析：首先根据三角形的各边都为正数，且周长为有理数可判断三角形的腰和底都为有理数，再根据等腰三角形的性质得出，底边上的高等于底边的一半，因为底边为有理数，所以高也为有理数，由此可判断出此题的正确答案．
解答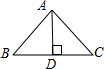：解：因为三角形的三边都必须为正数，且三边之和要为有理数，
所以三角形的三边都必须是有理数，即边AB，AC，BC都为有理数，
因为AD=BC，又根据等腰三角形三线合一的性质得到：
D为BC的中点，所以BD=DC=AD=BC，
所以BD，CD，AD都为有理数，即等腰三角形的腰和底边上的高都为有理数．
故选A
点评：此题考查等腰三角形的三线合一的性质，是一道把几何知识与代数知识融合在一块的综合题．