题目内容
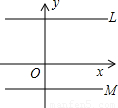
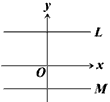
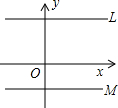 如图,坐标平面上有两直线L、M,其方程式分别为y=9、y=-6.若L上有一点P,M上有一点Q,PQ与y轴平行,且PQ上有一点R,PR:RQ=1:2,则R点与x轴的距离为何
如图,坐标平面上有两直线L、M,其方程式分别为y=9、y=-6.若L上有一点P,M上有一点Q,PQ与y轴平行,且PQ上有一点R,PR:RQ=1:2,则R点与x轴的距离为何
- A.1
- B.4
- C.5
- D.10
B
分析:由已知直线L上所有点的纵坐标为9,M上所由点的坐标为-6,由PQ与y轴平行即于x轴垂直,可得出PN=9,QN=6,PQ=PN+QN=9+6=15,根据已知PR:PQ=1:2可求出PR,从而求出R点与x轴的距离.
解答: 解:已知直线L和M的方程式是y=9、y=-6,
解:已知直线L和M的方程式是y=9、y=-6,
所以得到直线L、M都平行于x轴,
即得点P、Q到x轴的距离分别是9和6,
又PQ平行于y轴,所以PQ垂直于x轴,
所以,PN=9,QN=6,PQ=PN+QN=9+6=15,
又PR:RQ=1:2,
所以得:PR=5,PQ=10,
则,RN=PN-PR=9-5=4,
所以R点与x轴的距离为4.
故选:B.
点评:此题考查的知识点是坐标与图形性质,解题的关键是由已知直线L、M,及PQ与y轴平行先求出PQ,再由PR:PQ=1:2求出R点与x轴的距离.
分析:由已知直线L上所有点的纵坐标为9,M上所由点的坐标为-6,由PQ与y轴平行即于x轴垂直,可得出PN=9,QN=6,PQ=PN+QN=9+6=15,根据已知PR:PQ=1:2可求出PR,从而求出R点与x轴的距离.
解答:
 解:已知直线L和M的方程式是y=9、y=-6,
解:已知直线L和M的方程式是y=9、y=-6,所以得到直线L、M都平行于x轴,
即得点P、Q到x轴的距离分别是9和6,
又PQ平行于y轴,所以PQ垂直于x轴,
所以,PN=9,QN=6,PQ=PN+QN=9+6=15,
又PR:RQ=1:2,
所以得:PR=5,PQ=10,
则,RN=PN-PR=9-5=4,
所以R点与x轴的距离为4.
故选:B.
点评:此题考查的知识点是坐标与图形性质,解题的关键是由已知直线L、M,及PQ与y轴平行先求出PQ,再由PR:PQ=1:2求出R点与x轴的距离.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
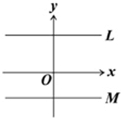 17、如图,坐标平面上有两直线L、M,其方程式分别为y=9、y=-6.若L上有一点P,M上有一点Q,PQ与y轴平行,且PQ上有一点R,PR:PQ=1:2,则R点与x轴的距离为何( )
17、如图,坐标平面上有两直线L、M,其方程式分别为y=9、y=-6.若L上有一点P,M上有一点Q,PQ与y轴平行,且PQ上有一点R,PR:PQ=1:2,则R点与x轴的距离为何( )