ЬтФПФкШн
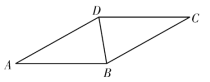
ЁОЬтФПЁПШчЭМ1ЃЌХзЮяЯпyЃНaЃЈx+2ЃЉЃЈxЉ6ЃЉЃЈaЃО0ЃЉгыxжсНЛгкCЃЌDСНЕуЃЈЕуCдкЕуDЕФзѓБпЃЉЃЌгыyжсИКАыжсНЛгкЕуAЃЎ
ЃЈ1ЃЉШєЁїACDЕФУцЛ§ЮЊ16ЃЎ
ЂйЧѓХзЮяЯпНтЮіЪНЃЛ
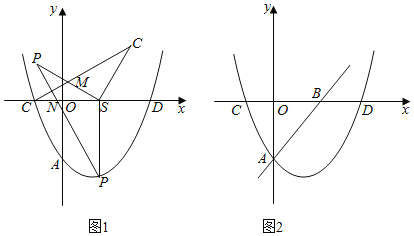
ЂкSЮЊЯпЖЮODЩЯвЛЕуЃЌЙ§SзїxжсЕФДЙЯпЃЌНЛХзЮяЯпгкЕуPЃЌНЋЯпЖЮSCЃЌSPШЦЕуSЫГЪБеыа§зЊШЮвтЯрЭЌЕФНЧЕНSC1ЃЌSP1ЕФЮЛжУЃЌЪЙЕуCЃЌPЕФЖдгІЕуC1ЃЌP1ЖМдкxжсЩЯЗНЃЌC1CгыP1SНЛгкЕуMЃЌP1PгыxжсНЛгкЕуNЃЎЧѓ![]() ЕФзюДѓжЕЃЛ
ЕФзюДѓжЕЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌжБЯпyЃНxЉ12aгыxжсНЛгкЕуBЃЌЕуMдкХзЮяЯпЩЯЃЌЧвТњзуЁЯMABЃН75ЁуЕФЕуMгаЧвжЛгаСНИіЃЌЧѓaЕФШЁжЕЗЖЮЇЃЎ
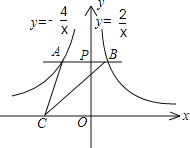
ЁОД№АИЁПЃЈ1ЃЉЂй![]() ЃЌЂкtЃН0ЪБЃЌ
ЃЌЂкtЃН0ЪБЃЌ![]() зюДѓжЕЮЊ2ЃЛЃЈ2ЃЉ
зюДѓжЕЮЊ2ЃЛЃЈ2ЃЉ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉЂйгЩЬтвтЃЌСюy=0ЃЌНтЕУCЃЈ-2ЃЌ0ЃЉЃЌDЃЈ6ЃЌ0ЃЉЕУCD=8ЃЌСюx=0ЃЌНтЕУy=-12aЃЌЧвa>0ЃЌAЃЈ0ЃЌ-12aЃЉЃЌМДOA=12aЃЌгЩSЁїACD=![]() =48a=16ЃЌНтЕУЃКaЃН
=48a=16ЃЌНтЕУЃКaЃН![]() ЃЌЫљЧѓХзЮяЯпЕФНтЮіЪНЮЊyЃН
ЃЌЫљЧѓХзЮяЯпЕФНтЮіЪНЮЊyЃН![]() (x+2)(x6)=
(x+2)(x6)= ![]() x2
x2![]() x4ЃЛ
x4ЃЛ
ЂкгЩгкЁЯSP1P-ЁЯSC1C=ЁЯSCC1ЃЌЧвЁЯMSC=ЁЯNSP1ЁрЁїMSCЁзЁїNSP1ЕУ![]() ЃЌЩшSЃЈtЃЌ0ЃЉЃЈ0ЁмtЁм6ЃЉЃЌдђSP=
ЃЌЩшSЃЈtЃЌ0ЃЉЃЈ0ЁмtЁм6ЃЉЃЌдђSP=![]() (t+2)(t6)ЃЌSC=t+2ЃЌ
(t+2)(t6)ЃЌSC=t+2ЃЌ![]() ПЩЕУt=0ЪБЃЌ
ПЩЕУt=0ЪБЃЌ![]() зюДѓжЕЮЊ2ЃЛ
зюДѓжЕЮЊ2ЃЛ
ЃЈ2ЃЉЗжСНжжЧщПіЬжТлЃЌЂйгЩжБЯпy=x-12aгыxжсНЛгкЕуBЕУBЃЈ12aЃЌ0ЃЉЃЌOA=OB=12aЃЌЁЯOAB=ЁЯOBA=45ЁуЃЌЕБЕуNдкyжсЕФзѓВрЪБЃЌДЫЪБЁЯMAO=30ЁуЕУжБЯпAMЕФНтЮіЪНЮЊЃК![]() ЕУЕуMЕФКсзјБъЮЊ
ЕУЕуMЕФКсзјБъЮЊ![]() ЕУ
ЕУ![]()
ЂкЕБЕуMдкyжсЕФгвВрЪБЃЌЙ§ЕуBзїxжсЕФДЙЯпгыЂйжажБЯпAEЙигкABЕФЖдГЦжБЯпНЛгкЕуFЃЌвзжЄЃКЁїEBAЁеЁїFBAЃЌЕУЁЯBAF=75ЁуЃЌBF=BE=![]() ЃЌЁЯFBO=90ЁуЃЌЕУжБЯпAFЕФНтЮіЪНЮЊЃК
ЃЌЁЯFBO=90ЁуЃЌЕУжБЯпAFЕФНтЮіЪНЮЊЃК![]() ЃЌЕуGКсзјБъЮЊ
ЃЌЕуGКсзјБъЮЊ![]() ЃЌЕуAЙигкХзЮяЯпЖдГЦжсx=2ЕФЖдГЦЕуЕФзјБъЮЊЃКЃЈ4ЃЌ-12aЃЉЃЌдђ
ЃЌЕуAЙигкХзЮяЯпЖдГЦжсx=2ЕФЖдГЦЕуЕФзјБъЮЊЃКЃЈ4ЃЌ-12aЃЉЃЌдђ![]() ЃЌЕУ
ЃЌЕУ![]() ЃЌвђДЫТњзуЁЯMAB=75ЁуЕФЕуMгаЧвжЛгаСНИіЃЌдђaЕФШЁжЕЗЖЮЇЮЊЃК
ЃЌвђДЫТњзуЁЯMAB=75ЁуЕФЕуMгаЧвжЛгаСНИіЃЌдђaЕФШЁжЕЗЖЮЇЮЊЃК![]() ЃЎ
ЃЎ
НтЃКЃЈ1ЃЉЂйгЩЬтвтЃЌСюyЃН0ЃЌНтЕУx1ЃНЉ2ЃЌx2ЃН6
ЁрCЃЈЉ2ЃЌ0ЃЉЃЌDЃЈ6ЃЌ0ЃЉ
ЁрCDЃН8ЃЎ
СюxЃН0ЃЌНтЕУyЃНЉ12aЃЌЧвaЃО0
ЁрAЃЈ0ЃЌЉ12aЃЉЃЌМДOAЃН12a
ЁрSЁїACDЃН![]() ЃН48aЃН16ЃЌ
ЃН48aЃН16ЃЌ
НтЕУЃК![]()
ЫљЧѓХзЮяЯпЕФНтЮіЪНЮЊ![]() ЃН
ЃН![]()
ЂкгЩЬтвтжЊЃЌЁЯSP1PЉЁЯSC1CЃНЁЯSCC1ЃЌЧвЁЯMSCЃНЁЯNSP1
ЁрЁїMSCЁзЁїNSP1
Ёр![]()
ЩшSЃЈtЃЌ0ЃЉЃЈ0ЁмtЁм6ЃЉЃЌдђSPЃН![]() ЃЌSCЃНt+2
ЃЌSCЃНt+2
Ёр![]()
Ёп0ЁмtЁм6
ЁрtЃН0ЪБЃЌ![]() зюДѓжЕЮЊ2ЃЛ
зюДѓжЕЮЊ2ЃЛ
ЃЈ2ЃЉгЩЬтвтЃЌжБЯпyЃНxЉ12aгыxжсНЛгкЕуBЕУBЃЈ12aЃЌ0ЃЉЃЌOAЃНOBЃН12aЃЌЁЯOABЃНЁЯOBAЃН45Ёу
ШчЭМ2
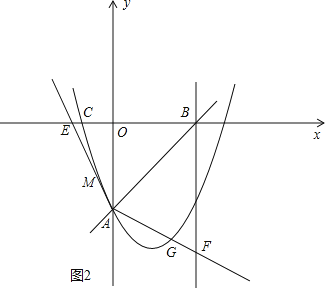
ЕБЕуMдкyжсЕФзѓВрЪБЃЌДЫЪБЁЯMAOЃН30Ёу
ЩшжБЯпAMгыxжсНЛгкЕуEЃЌдђOEЃН![]()
Ёр![]()
гжЁпAЃЈ0ЃЌЉ12aЃЉЃЌ
ЁржБЯпAMЕФНтЮіЪНЮЊЃК![]()
гЩ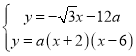 ЕУЃК
ЕУЃК![]()
НтЕУЃК![]()
ЁрЕуMЕФКсзјБъЮЊ![]()
Ёп![]()
![]()
ЂкЕБЕуMдкyжсЕФгвВрЪБЃЌЙ§ЕуBзїxжсЕФДЙЯпгыЂйжажБЯпAEЙигкABЕФЖдГЦжБЯпНЛгкЕуFЃЌ
взжЄЃКЁїEBAЁеЁїFBAЃЌ
ЕУЁЯBAFЃН75ЁуЃЌBFЃНBEЃН![]() ЃЌЁЯFBOЃН90Ёу
ЃЌЁЯFBOЃН90Ёу
Ёр![]()
ЁржБЯпAFЕФНтЮіЪНЮЊЃК![]()
гЩ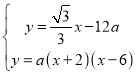 ЃЌНтЕУЃК
ЃЌНтЕУЃК![]()
ЁрЕуGКсзјБъЮЊ![]() ЃЌ
ЃЌ
ЕуAЙигкХзЮяЯпЖдГЦжсxЃН2ЕФЖдГЦЕуЕФзјБъЮЊЃКЃЈ4ЃЌЉ12aЃЉЃЌ
дђ![]() ЃЌЕУ
ЃЌЕУ![]() ЃЌ
ЃЌ
ЙЪвЊЪЙТњзуЁЯMABЃН75ЁуЕФЕуMгаЧвжЛгаСНИіЃЌдђaЕФШЁжЕЗЖЮЇЮЊЃК![]() ЃЎ
ЃЎ

 ПМЧАБиСЗЯЕСаД№АИ
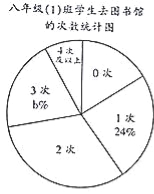
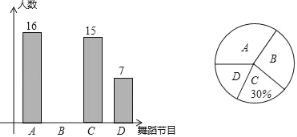
ПМЧАБиСЗЯЕСаД№АИЁОЬтФПЁПДяжнЪаЭМЪщЙнНёФъ4дТ23ШеПЊЗХвдРДЃЌЪмЕНЪаУёЕФЙуЗКЙизЂ.5дТЕзЃЌАЫФъМЖЃЈ1ЃЉАрбЇЩњаЁгБЖдШЋАрЭЌбЇетвЛИіЖрдТРДШЅаТЭМЪщЙнЕФДЮЪ§зіСЫЕїВщЭГМЦЃЌВЂжЦГЩСЫШчЭМВЛЭъећЕФЭГМЦЭМБэЃЎ
АЫФъМЖЃЈ1ЃЉАрбЇЩњШЅаТЭМЪщЙнЕФДЮЪ§ЭГМЦБэ
ШЅЭМЪщЙнЕФДЮЪ§ | 0ДЮ | 1ДЮ | 2ДЮ | 3ДЮ | 4ДЮМАвдЩЯ |
ШЫЪ§ | 8 | 12 | a | 10 | 4 |
ЧыФуИљОнЭГМЦЭМБэжаЕФаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЬюПеЃКa= ЃЌb= ЃЛ
ЃЈ2ЃЉЧѓЩШаЮЭГМЦЭМжаЁА0ДЮЁБЕФЩШаЮЫљеМдВаФНЧЕФЖШЪ§ЃЛ
ЃЈ3ЃЉДгШЋАрШЅЙ§ИУЭМЪщЙнЕФЭЌбЇжаЫцЛњГщШЁ1ШЫЃЌЬИЬИЖдаТЭМЪщЙнЕФгЁЯѓКЭИаЪмЃЎЧѓЧЁКУГщжаШЅЙ§ЁА4ДЮМАвдЩЯЁБЕФЭЌбЇЕФИХТЪЃЎ