Question

2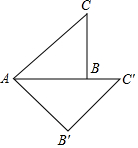．如图，已知△ABC是等腰直角三角形，以点A为中心，将△ABC顺时针旋转45°，得到△AB′C′，则∠CAB′的度数为（　　）

• A． 45°
• B． 60°
• C． 75°
• D． 90°

Answer 1

分析 根据等腰直角三角形的性质∠BAC=45°，根据旋转的性质可得∠B′AC′=∠BAC，∠CAC′=45°，然后求解即可．

解答 解：∵△ABC是等腰直角三角形，
∴∠BAC=45°，
∵以点A为中心，将△ABC顺时针旋转45°，得到△AB′C′，
∴∠B′AC′=∠BAC=45°，∠CAC′=45°，
∴∠CAB′=∠CAC′+∠B′AC′=45°+45°=90°．
故选D．

点评 本题考查了旋转的性质，旋转变换只改变图形的位置不改变图形的形状与大小，旋转前后的对应角相等，对应边相等．