题目内容
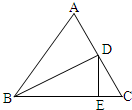6、如图所示，△ABC是等边三角形，BD是中线，DE⊥BC于E．若EC=2，则BE=（ ）分析：过点A作AM⊥BC于点M，即DE∥AM，由于△ABC为等边三角形，可知点M为BC边的中点，D为AC的中点，根据中位线定理，可知CM=2CE，从而得出BC的长，即可得出BE的长．
解答：解：过点A作AM垂直BC于点M（如下图所示），
根据题意可得，DE∥AM，
又△ABC是等边三角形，即D和M分别是AC和BC的中点，
在△AMC中，DE为中位线，
即有MC=2EC=4，
故BC=8，
所以BE=BC-EC=6．
故选C．
根据题意可得，DE∥AM，
又△ABC是等边三角形，即D和M分别是AC和BC的中点，
在△AMC中，DE为中位线，
即有MC=2EC=4，
故BC=8，
所以BE=BC-EC=6．
故选C．
点评：本题主要考查了等边三角形的性质以及三角形中位线定理知识的运用，题目不难，适合作为学生平时练习的题目．
练习册系列答案
小学夺冠AB卷系列答案
ABC考王全优卷系列答案
相关题目
22、如图所示，△ABC是等边三角形，延长BC至E，延长BA至F，使AF=BE，连接CF、EF，过点F作直线FD⊥CE于D，试发现∠FCE与∠FEC的数量关系，并说明理由．
7、如图所示，△ABC是正三角形，△A1B1 C1的三条边A1B1、BlC1、C1A1交△ABC各边分别于C2、C3，A2、A3，B2、B3．已知A2C3=C2B3=B2A3，且C2C32+B2B32=A2A32．请你证明：AlB1⊥C1A1．
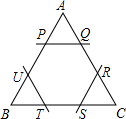如图所示，△ABC是边长为a的正三角形纸张，今在各角剪去一个三角形，使得剩下的六边形PQRSTU为正六边形，则此正六边形的周长为何（ ）| A、2a | ||
| B、3a | ||
C、
| ||
D、
|
12、如图所示，△ABC是等边三角形，AQ=PQ，PR⊥AB于R点，PS⊥AC于S点，PR=PS，则四个结论：①点P在∠A的平分线上；②AS=AR；③QP∥AR；④△BRP≌△QSP，正确的结论是（ ）
（2012•黄陂区模拟）如图所示，△ABC是⊙O的内接正三角形，四边形DEFG是⊙O的内接正方形，EF∥BC，则∠AOF为（ ）