题目内容
【题目】如图，已知矩形ABCD，点E在边AD上，连接BE将△ABE沿BE翻折，得到△MBE，M点刚好在CD边上，若AD长为2，AB长为
，则AE＝_____．
【答案】
．
【解析】
由矩形的性质得出BC＝AD＝2，CD＝AB＝
，∠C＝∠D＝90°，由折叠的性质得MB＝AB＝，ME＝AE，由勾股定理得出CM＝
，得出DM＝CD﹣CM＝1，设ME＝AE＝x，则DE＝2﹣x，在Rt△DEM中，由勾股定理得出方程，解方程即可．
解：∵四边形ABCD是矩形，
∴BC＝AD＝2，CD＝AB＝，∠C＝∠D＝90°，
由折叠的性质得：MB＝AB＝，ME＝AE，
∴CM＝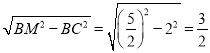
，
∴DM＝CD﹣CM＝﹣
＝1，
设ME＝AE＝x，则DE＝2﹣x，
在Rt△DEM中，由勾股定理得：12+（2﹣x）2＝x2，
解得：x＝，即AE＝，
故答案为：．
练习册系列答案
相关题目
