Question

【题目】如图，AB是半圆O的直径，点C圆外一点，OC垂直于弦AD，垂足为点F，OC交⊙O于点E，连接AC，∠BED＝∠C．

（1）判断AC与⊙O的位置关系，并证明你的结论；

（2）是否存在BE平分∠OED的情況？如果存在，求此时∠C的度数；如果不存在，说明理由．

Answer 1

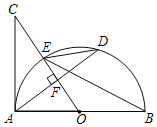
【答案】（1）AC与⊙O相切，见解析；（2）∠C＝30°

【解析】

（1）由于OC⊥AD，那么∠OAD+∠AOC=90°，又∠BED=∠BAD，且∠BED=∠C，于是∠OAD=∠C，从而有∠C+∠AOC=90°，再利用三角形内角和定理，可求∠OAC=90°，即AC是⊙O的切线．

（2）证明∠AOC=2∠C，再利用三角形内角和定理即可解决问题．

（1）AC与⊙O相切．理由如下：

∵OC⊥AD，

∴∠AOC+∠BAD=90°．

又∵∠C=∠BED=∠BAD，

∴∠AOC+∠C=90°．

∴AB⊥AC，

∴AC与⊙O相切．

（2）存在．

∵OE=OB，

∴∠OEB=∠OBE．

∵∠C=∠BED=∠BEO，∠AOC=∠OEB+∠OBE，

∴∠AOC=2∠C．

∵∠AOC+∠C=90°，

∴2∠C+∠C=90°，

∴∠C=30°．