题目内容
已知:抛物线y=-x2+bx+c经过B(3,0)、C(0,3)两点,顶点为A.
求:(1)抛物线的表达式;
(2)顶点A的坐标.
解:(1)把B(3,0)、C(0,3)代入y=-x2+bx+c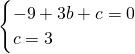 ,
,
解得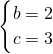 .
.
故抛物线的解析式为y=-x2+2x+3;
(2)y=-x2+2x+3
=-(x2-2x+1)+3+1
=-(x-1)2+4,
所以顶点A的坐标为(1,4).
分析:(1)直接把B(3,0)、C(0,3)代入y=-x2+bx+c得到关于b、c的方程组,解方程组求出b、c,可确定抛物线的解析式;
(2)把(1)的解析式进行配方可得到顶点式,然后写出顶点坐标即可.
点评:本题考查了待定系数法求二次函数的解析式:先设抛物线的解析式(一般式、顶点式或交点式),再把抛物线上的点的坐标代入得到方程组,然后解方程可确定抛物线的解析式.也考查了二次函数的性质.
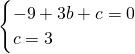 ,
,解得
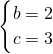 .
.故抛物线的解析式为y=-x2+2x+3;
(2)y=-x2+2x+3
=-(x2-2x+1)+3+1
=-(x-1)2+4,
所以顶点A的坐标为(1,4).
分析:(1)直接把B(3,0)、C(0,3)代入y=-x2+bx+c得到关于b、c的方程组,解方程组求出b、c,可确定抛物线的解析式;
(2)把(1)的解析式进行配方可得到顶点式,然后写出顶点坐标即可.
点评:本题考查了待定系数法求二次函数的解析式:先设抛物线的解析式(一般式、顶点式或交点式),再把抛物线上的点的坐标代入得到方程组,然后解方程可确定抛物线的解析式.也考查了二次函数的性质.

练习册系列答案
相关题目
已知:抛物线y=x2-6x+c的最小值为1,那么c的值是( )
| A、10 | B、9 | C、8 | D、7 |