题目内容
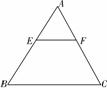
 设三角形ABC为一等腰直角三角形,角ABC为直角,D为AC中点.以B为圆心,AB为半径作一圆弧AFC,以D为中心,AD为半径,作一半圆AGC,作正方形BDCE.月牙形AGCFA的面积与正方形BDCE的面积大小关系( )
设三角形ABC为一等腰直角三角形,角ABC为直角,D为AC中点.以B为圆心,AB为半径作一圆弧AFC,以D为中心,AD为半径,作一半圆AGC,作正方形BDCE.月牙形AGCFA的面积与正方形BDCE的面积大小关系( )分析:首先利用扇形公式计算出第一个扇形的面积,再利用月牙形等于扇形-三角形的关系求出月牙形的面积,进行比较得出它们的面积关系.
解答:解:设半径为r,则正方形BDCE的面积为r2,
月牙形AGCFA的面积=
πr2-[
π(
r)2-
×2r•r]
=
πr2-[
πr2-r2]
=r2.
则月牙形AGCFA的面积与正方形BDCE的面积大小关系为:S月牙=S正方形.
故选A.
月牙形AGCFA的面积=
| 1 |
| 2 |
| 1 |
| 4 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
=r2.
则月牙形AGCFA的面积与正方形BDCE的面积大小关系为:S月牙=S正方形.
故选A.
点评:本题的关键是算出三个图形的面积,首先利用扇形公式计算出第一个扇形的面积,再利用月牙形等于扇形-三角形的关系求出月牙形的面积,进行比较得出它们的面积关系.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
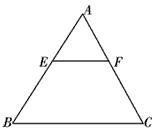
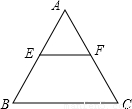
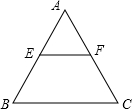 已知:如图,一等边三角形ABC纸片的边长为2a,E是AB边上一动点,(点E与点A、B不重合),过点E作EF∥BC,交AC于点F,设EF=x.
已知:如图,一等边三角形ABC纸片的边长为2a,E是AB边上一动点,(点E与点A、B不重合),过点E作EF∥BC,交AC于点F,设EF=x.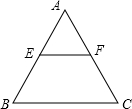 已知:如图,一等边三角形ABC纸片的边长为2a,E是AB边上一动点,(点E与点A、B不重合),过点E作EF∥BC,交AC于点F,设EF=x.
已知:如图,一等边三角形ABC纸片的边长为2a,E是AB边上一动点,(点E与点A、B不重合),过点E作EF∥BC,交AC于点F,设EF=x.