题目内容
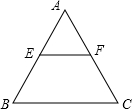 已知:如图,一等边三角形ABC纸片的边长为2a,E是AB边上一动点,(点E与点A、B不重合),过点E作EF∥BC,交AC于点F,设EF=x.
已知:如图,一等边三角形ABC纸片的边长为2a,E是AB边上一动点,(点E与点A、B不重合),过点E作EF∥BC,交AC于点F,设EF=x.(1)用x的代数式表示△AEF的面积;
(2)将△AEF沿EF折叠,折叠后与四边形BCFE重叠部分的面积为y,求出y关于x的函数关系式,并写出自变量x的取值范围.
分析:(1)首先根据等边三角形的性质求得大等边三角形的高,进一步求得其面积.再根据相似三角形的面积比是相似比的平方,求得△AEF的面积;
(2)此题应分两种情况考虑:当折叠后△AEF的顶点A落在四边形BCFE内或BC边上时,重叠部分的面积即是三角形AEF的面积;当叠后△AEF的顶点A落在四边形BCFE外点A′处时,重叠部分的面积即是三角形AEF的面积减去A′MN的面积,根据轴对称的性质和相似三角形的性质进行计算.
(2)此题应分两种情况考虑:当折叠后△AEF的顶点A落在四边形BCFE内或BC边上时,重叠部分的面积即是三角形AEF的面积;当叠后△AEF的顶点A落在四边形BCFE外点A′处时,重叠部分的面积即是三角形AEF的面积减去A′MN的面积,根据轴对称的性质和相似三角形的性质进行计算.
解答: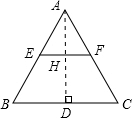 解:(1)在等边△ABC中,
解:(1)在等边△ABC中,
作AD⊥BC于D,交EF于H,
∴BD=DC=
BC=a.
又∵tan∠ABD=tan60°=
,
∴AD=
a.(1分)
∵EF∥BC,
∴△AEF∽△ABC.
∴
=
,
=
.
∴AH=
x.(2分)
∴S△AEF=
AH×EF.
S△AEF=
x2=
x2.(3分)
(2)①当折叠后△AEF的顶点A落在四边形BCFE内或BC边上时
y=
x2(0<x≤a).(4分)
②当折叠后△AEF的顶点A落在四边形BCFE外点A′处时,
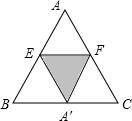
A′F交BC于M,A′E交BC于N,连接AA′交EF于H,交BC于D,
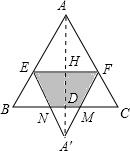
∴
=
∴
=
,
又∵AH=A′H,
∴
=
,
∴
=
,
∴
=(
)2(5分)
=
,
∴S△A’MN=
(2x-2a)2.
∴S四边形MFEN=
x2-
(2x-2a)2.(6分)
∴y=-
x2+2
ax-
a2(a<x<2a).(7分)
 解:(1)在等边△ABC中,
解:(1)在等边△ABC中,作AD⊥BC于D,交EF于H,
∴BD=DC=
| 1 |
| 2 |
又∵tan∠ABD=tan60°=
| AD |
| BD |
∴AD=
| 3 |
∵EF∥BC,
∴△AEF∽△ABC.
∴
| AH |
| AD |
| EF |
| BC |
| AH | ||
|
| x |
| 2a |
∴AH=
| ||
| 2 |
∴S△AEF=
| 1 |
| 2 |
S△AEF=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
(2)①当折叠后△AEF的顶点A落在四边形BCFE内或BC边上时
y=
| ||
| 4 |
②当折叠后△AEF的顶点A落在四边形BCFE外点A′处时,

A′F交BC于M,A′E交BC于N,连接AA′交EF于H,交BC于D,

∴
| AH |
| AD |
| x |
| 2a |
∴
| AH |
| HD |
| x |
| 2a-x |
又∵AH=A′H,
∴
| A′H |
| HD |
| x |
| 2a-x |
∴
| A′H |
| A′D |
| x |
| 2x-2a |
∴
| S△A′EF |
| S△A′MN |
| x |
| 2x-2a |
| ||||
| S△A′MN |
| x2 |
| (2x-2a)2 |
∴S△A’MN=
| ||
| 4 |
∴S四边形MFEN=
| ||
| 4 |
| ||
| 4 |
∴y=-
3
| ||
| 4 |
| 3 |
| 3 |
点评:此题综合运用了相似三角形的性质、等边三角形的性质和轴对称的性质.特别注意第2小题的两种情况.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
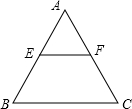 已知:如图,一等边三角形ABC纸片的边长为2a,E是AB边上一动点,(点E与点A、B不重合),过点E作EF∥BC,交AC于点F,设EF=x.
已知:如图,一等边三角形ABC纸片的边长为2a,E是AB边上一动点,(点E与点A、B不重合),过点E作EF∥BC,交AC于点F,设EF=x.