题目内容
如图：△ABC中，AB=AC，∠A=120°，将△ABC绕着点B顺时针旋转，使点A落在BC边上的点A′处，点C落在点C处，那么∠BCC′的度数是________．
75°
分析：先根据等腰三角形的性质得出∠ABC的度数，再根据图形旋转的性质得出∠CBC′=∠ABC，BC=BC′，再根据等腰三角形的性质即可得出∠BCC′的度数．
解答：∵△ABC中，AB=AC，∠A=120°，
∴∠ABC=
=
=30°，
∵△A′BC′由△ABC旋转而成，
∴∠CBC′=∠ABC=30°，BC=BC′，
∴∠BCC′=
=
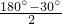=75°．
故答案为：75°．
点评：本题考查的是旋转的性质，熟知图形旋转不变性的性质是解答此题的关键．
分析：先根据等腰三角形的性质得出∠ABC的度数，再根据图形旋转的性质得出∠CBC′=∠ABC，BC=BC′，再根据等腰三角形的性质即可得出∠BCC′的度数．
解答：∵△ABC中，AB=AC，∠A=120°，
∴∠ABC=
==30°，∵△A′BC′由△ABC旋转而成，
∴∠CBC′=∠ABC=30°，BC=BC′，
∴∠BCC′=
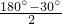==75°．故答案为：75°．
点评：本题考查的是旋转的性质，熟知图形旋转不变性的性质是解答此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
26、已知：如图，△ABC中，点D在AC的延长线上，CE是∠DCB的角平分线，且CE∥AB．
27、已知：如图，△ABC中，∠BAC=60°，D、E两点在直线BC上，连接AD、AE．
27、如图，△ABC中，AD⊥BC于D，DN⊥AC于N，DM⊥AB于M
14、如图，△ABC中，∠BAC=120°，AD⊥BC于D，且AB+BD=DC，则∠C的大小是（ ）
已知，如图，△ABC中，点D在BC上，且∠1=∠C，∠2=2∠3，∠BAC=70°．