题目内容
 如图,某菜农搭建了一个横截面为抛物线的大棚,大棚在地面上的宽为AB(单位:米),AB=10,以AB所在直线为x轴,以AB垂直平分线为y轴建立的平面直角坐标系,y轴与抛物线交于点C,抛物线解析式为y=-
如图,某菜农搭建了一个横截面为抛物线的大棚,大棚在地面上的宽为AB(单位:米),AB=10,以AB所在直线为x轴,以AB垂直平分线为y轴建立的平面直角坐标系,y轴与抛物线交于点C,抛物线解析式为y=- x2+h.
x2+h.
(1)求点C坐标;
(2)若菜农身高为 米,则在她直立的情况下,在大棚内的横向活动范围有几米?
米,则在她直立的情况下,在大棚内的横向活动范围有几米?
解:(1)∵BO= =
=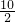 =5,
=5,
∴B(5,0),
把B(5,0)代入y=- x2+h,
x2+h,
0=- ×52+h,
×52+h,
解得:h= ,
,
当x=0时,y=- ×02+
×02+ =
= ,
,
∴C(0, );
);
(2)当y= 时,
时, =-
=- x2+
x2+ ,
,
解得:x1=3,x2=-3,
∴3+3=6(m),
∴在她直立的情况下,在大棚内的横向活动范围有6米.
分析:(1)首先利用AB的长得出B点坐标,再将B点坐标代入解析式求出h的值,进而求出C点坐标;
(2)当y= 时,得出
时,得出 =-
=- x2+
x2+ ,进而求出横向活动范围.
,进而求出横向活动范围.
点评:此题主要考查了二次函数的应用,根据已知件得出B点坐标是解题关键.
 =
=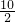 =5,
=5,∴B(5,0),
把B(5,0)代入y=-
 x2+h,
x2+h,0=-
 ×52+h,
×52+h,解得:h=
 ,
,当x=0时,y=-
 ×02+
×02+ =
= ,
,∴C(0,
 );
);(2)当y=
 时,
时, =-
=- x2+
x2+ ,
,解得:x1=3,x2=-3,
∴3+3=6(m),
∴在她直立的情况下,在大棚内的横向活动范围有6米.
分析:(1)首先利用AB的长得出B点坐标,再将B点坐标代入解析式求出h的值,进而求出C点坐标;
(2)当y=
 时,得出
时,得出 =-
=- x2+
x2+ ,进而求出横向活动范围.
,进而求出横向活动范围.点评:此题主要考查了二次函数的应用,根据已知件得出B点坐标是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,某菜农要修建一个育苗棚,棚宽a=12m,高b=5m,长d=20m,请你帮他算一下覆盖在顶上的塑料薄膜需多少?
如图,某菜农要修建一个育苗棚,棚宽a=12m,高b=5m,长d=20m,请你帮他算一下覆盖在顶上的塑料薄膜需多少?