题目内容
多项式x2+mx+5因式分解得（x+5）（x+n），则m=________，n=________．
6 1
分析：将（x+5）（x+n）展开，得到，使得x2+（n+5）x+5n与x2+mx+5的系数对应相等即可．
解答：∵（x+5）（x+n）=x2+（n+5）x+5n，
∴x2+mx+5=x2+（n+5）x+5n
∴
，
∴
，
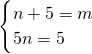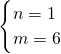故答案为6，1．
点评：本题考查了因式分解的意义，使得系数对应相等即可．
分析：将（x+5）（x+n）展开，得到，使得x2+（n+5）x+5n与x2+mx+5的系数对应相等即可．
解答：∵（x+5）（x+n）=x2+（n+5）x+5n，
∴x2+mx+5=x2+（n+5）x+5n
∴
，∴
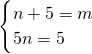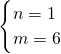，故答案为6，1．
点评：本题考查了因式分解的意义，使得系数对应相等即可．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目