题目内容
如图,在平面直角坐标系中,点A的坐标(﹣2,0),△ABO是直角三角形,∠AOB=60°.现将Rt△ABO绕原点O按顺时针方向旋转到Rt△A′B′O的位置,则此时边OB扫过的面积为 .

 π .
π .
【考点】扇形面积的计算;坐标与图形性质;旋转的性质.
【分析】根据点A的坐标(﹣2,0),可得OA=2,再根据含30°的直角三角形的性质可得OB的长,再根据性质的性质和扇形的面积公式即可求解.
【解答】解:∵点A的坐标(﹣2,0),
∴OA=2,
∵△ABO是直角三角形,∠AOB=60°,
∴∠OAB=30°,
∴OB=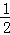 OA=1,
OA=1,
∴边OB扫过的面积为: =
= π.
π.
故答案为: π.
π.
【点评】本题考查了扇形的面积公式:S= ,其中n为扇形的圆心角的度数,R为圆的半径),或S=
,其中n为扇形的圆心角的度数,R为圆的半径),或S=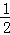 lR,l为扇形的弧长,R为半径.
lR,l为扇形的弧长,R为半径.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
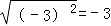 A.
A. 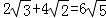 B.
B. 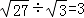 C.
C. 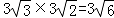 D.
D. 与y=﹣kx2+k(k≠0)在同一直角坐标系中的图象可能是( )
与y=﹣kx2+k(k≠0)在同一直角坐标系中的图象可能是( ) B.
B. C.
C. D.
D.

 B.
B. C.
C. D.
D.
 的相反数的是
的相反数的是
 B.
B. C.
C. D.
D.