题目内容
10. 已知:如图,AB∥CD,E是AB的中点,CE=DE.求证:
已知:如图,AB∥CD,E是AB的中点,CE=DE.求证:(1)∠AEC=∠BED;
(2)AC=BD.
分析 (1)根据CE=DE得出∠ECD=∠EDC,再利用平行线的性质进行证明即可;
(2)根据SAS证明△AEC与△BED全等,再利用全等三角形的性质证明即可.
解答 证明:(1)∵AB∥CD,
∴∠AEC=∠ECD,∠BED=∠EDC,
∵CE=DE,
∴∠ECD=∠EDC,
∴∠AEC=∠BED;
(2)∵E是AB的中点,
∴AE=BE,
在△AEC和△BED中,
$\left\{\begin{array}{l}{AE=BE}\\{∠AEC=∠BED}\\{EC=ED}\end{array}\right.$,
∴△AEC≌△BED(SAS),
∴AC=BD.
点评 本题主要考查了全等三角形的判定以及全等三角形的性质,关键是根据SAS证明全等.

练习册系列答案
相关题目
18.函数y=$\sqrt{x-4}$中自变量x的取值范围是( )
| A. | x>4 | B. | x≥4 | C. | x≤4 | D. | x≠4 |
2.下列计算正确的是( )
| A. | (a5)2=a10 | B. | x16÷x4=x4 | C. | 2a2+3a2=6a4 | D. | b3•b3=2b3 |
19.某市在一次扶贫助残活动中,共捐款5280000元,将5280000用科学记数法表示为( )
| A. | 5.28×106 | B. | 5.28×107 | C. | 52.8×106 | D. | 0.528×107 |
11.如图,是一个几何体的三视图(主视图中的弧线是半圆),则该几何体的体积是( )

| A. | π | B. | 2π | C. | 4π | D. | 8π |
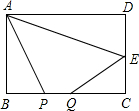 如图,矩形ABCD中,AB=8,BC=16,E为CD的中点,点P、Q为BC上两个动点,
如图,矩形ABCD中,AB=8,BC=16,E为CD的中点,点P、Q为BC上两个动点, 一次函数y=$\frac{3}{4}$x的图象如图所示,它与二次函数y=ax2-4ax+c的图象交于A、B两点(其中点A在点B的左侧),与这个二次函数图象的对称轴交于点C.
一次函数y=$\frac{3}{4}$x的图象如图所示,它与二次函数y=ax2-4ax+c的图象交于A、B两点(其中点A在点B的左侧),与这个二次函数图象的对称轴交于点C.