题目内容
【题目】矩形ABCD中,CE平分∠BCD,交直线AD于点E,若CD=6,AE=2,则tan∠ACE=______.
【答案】![]() 或
或![]()
【解析】(1)如图1,当点E在线段AD上时,
∵在矩形ABCD中,AD∥BC,CE平分∠BCD,
∴∠DEC=∠BCE=∠DCE,
∴DE=CD=6,
∵AE=2,
∴AD=6+2=8,
∴在Rt△ACD中,AC=10,
过点E作EF⊥AC于点F,
则由sin∠EAF=![]() ,可得EF=
,可得EF=![]() ,AF=
,AF=![]() ,
,
∴CF=![]() ,
,
∴tan∠ACE=![]() ;
;
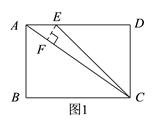
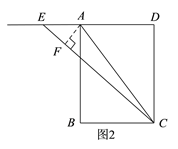
(2)如图2,当点E在DA的延长线上时,过点A作AF⊥EC于点F,
∵在矩形ABCD中,AD∥BC,CE平分∠BCD,
∴∠DEC=∠BCE=∠DCE,
∴DE=CD=6,
∵∠D=90°,
∴CE=![]() ,∠AEF=∠EAF=45°,
,∠AEF=∠EAF=45°,
∵AE=2,
∴EF=AF=![]() ,
,
∴FC=CE-EF=![]() ,
,
∴tan∠ACE=![]() .
.
综上所述,tan∠ACE=![]() 或
或![]() .
.
故答案为: ![]() 或
或![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案
相关题目