题目内容
13.将4个数a,b,c,d排成2行、2列,两边各加一条竖直线记成$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$,定义$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=ad-bc,若$|\begin{array}{l}{-5}&{3{x}^{2}+5}\\{2}&{{x}^{2}-3}\end{array}|$=6,则11x2-5=-6.分析 根据题意列出整式相加减的式子,进而可得出结论.
解答 解:∵$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=ad-bc,
∴-5(x2-3)-2(3x2+5)=6,
∴11x2-5=-6.
故答案为:-6.
点评 本题考查的是整式的加减,熟知整式的加减实质上就是合并同类项是解答此题的关键.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
3.若函数y=$(3-m){x^{{m^2}-8}}$是正比例函数,则常数m的值是( )
| A. | -$\sqrt{7}$ | B. | ±$\sqrt{7}$ | C. | ±3 | D. | -3 |
3.方程$\frac{2x-1}{3}$=x-2的解是( )
| A. | x=5 | B. | x=-5 | C. | x=2 | D. | x=-2 |
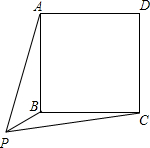 点P是正方形ABCD外一点,PB=12cm,△APB的面积是90cm2,△CPB的面积是48cm2.请你回答:正方形ABCD的面积是多少cm2?
点P是正方形ABCD外一点,PB=12cm,△APB的面积是90cm2,△CPB的面积是48cm2.请你回答:正方形ABCD的面积是多少cm2?