题目内容
19．计算：-$\sqrt{8}$+|-$\sqrt{2}$|+2sin45°+π0+（$\frac{1}{2}$）-1．分析 原式第一项化为最简二次根式，第二项利用绝对值的代数意义化简，第三项利用特殊角的三角函数值计算，第四项利用零指数幂法则计算，最后一项利用负整数指数幂法则计算即可得到结果．
解答 解：原式=-2$\sqrt{2}$+$\sqrt{2}$+2×$\frac{\sqrt{2}}{2}$+1+2=3．
点评 此题考查了实数的运算，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
10．我们解一元二次方程3x2-6x=0时，可以运用因式分解法，将此方程化为3x（x-2）=0，从而得到两个一元一次方程：3x=0或x-2=0，进而得到原方程的解为x1=0，x2=2．这种解法体现的数学思想是（ ）
| A． | 转化思想 | B． | 函数思想 | C． | 数形结合思想 | D． | 公理化思想 |
14．下列运算正确的是（ ）
| A． | 4m-m=3 | B． | 2m2•m3=2m5 | C． | （-m3）2=m9 | D． | -（m+2n）=-m+2n |
4．
已知，AC∥ED，∠C=26°，∠CBE=37°，则∠BED的度数是（ ）
已知，AC∥ED，∠C=26°，∠CBE=37°，则∠BED的度数是（ ）| A． | 53° | B． | 63° | C． | 73° | D． | 83° |
11．下列说法正确的是（ ）
| A． | 1的相反数是-1 | B． | 1的倒数是-1 | C． | 1的立方根是±1 | D． | -1是无理数 |
8．
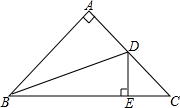如图，在△ABC中，∠BAC=90°，AB=AC，点D为边AC的中点，DE⊥BC于点E，连接BD，则tan∠DBC的值为（ ）
如图，在△ABC中，∠BAC=90°，AB=AC，点D为边AC的中点，DE⊥BC于点E，连接BD，则tan∠DBC的值为（ ）| A． | $\frac{1}{3}$ | B． | $\sqrt{2}$-1 | C． | 2-$\sqrt{3}$ | D． | $\frac{1}{4}$ |