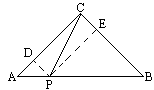
题目内容
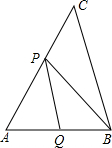如图，已知：AP2=AQ•AB，且∠ABP=∠C，试说明△QPB∽△PBC．
证明：∵AP2=AQ•AB，
∴
=
，
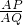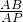∵∠A=∠A，
∴△APQ∽△ABP，
∴∠APB=∠AQP，
又∵∠ABP=∠C，
∴△QPB∽△PBC．
分析：首先利用相似三角形的判定得出△APQ∽△ABP，进而得出∠APB=∠AQP，利用两角相等得出△QPB∽△PBC．
点评：此题主要考查了相似三角形的判定与性质，利用已知得出△APQ∽△ABP得出∠APB=∠AQP是解题关键．
∴
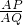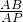=，∵∠A=∠A，
∴△APQ∽△ABP，
∴∠APB=∠AQP，
又∵∠ABP=∠C，
∴△QPB∽△PBC．
分析：首先利用相似三角形的判定得出△APQ∽△ABP，进而得出∠APB=∠AQP，利用两角相等得出△QPB∽△PBC．
点评：此题主要考查了相似三角形的判定与性质，利用已知得出△APQ∽△ABP得出∠APB=∠AQP是解题关键．
练习册系列答案
超能学典应用题题卡系列答案
相关题目
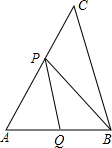如图，已知：AP2=AQ•AB，且∠ABP=∠C，试说明△QPB∽△PBC．
，AB＝8，CD＝6，BC＝
．在AB边上取动点P，连结DP，作PQ⊥DP，使PQ交射线BC于点E．设AP＝x，BE＝y．