题目内容
如图，已知0A⊥m，OB⊥m，所以OA与OB重合，其理由是（ ）分析：根据平面内，经过一点有且只有一条直线与已知直线垂直可得OA与OB重合．
解答：解：根据垂线的性质：平面内，过一点有且只有一条直线与已知直线垂直可得OA与OB重合，
故选：C．
故选：C．
点评：此题主要考查了垂线的性质，关键掌握平面内，过一点有且只有一条直线与已知直线垂直可得OA与OB重合，注意：“有且只有”中，“有”指“存在”，“只有”指“唯一”．
练习册系列答案
相关题目
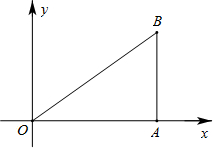个单位的速度向x轴负方向作匀速平移运动．若它们同时出发，运动的时间为t秒，当点P运动到O时，它们都停止运动．
如图，已知长方形ABC0中，边AB=8，BC=4．以点0为原点，0A、OC所在的直线为y轴和x轴建立直角坐标系．
如图，已知0A⊥m，OB⊥m，所以OA与OB重合，其理由是