题目内容
10.如图甲,对于平面上不大于90°的∠MON,我们给出如下定义:如果点P在∠MON的内部,作PE⊥OM,PF⊥ON,垂足分别为点E、F,那么称PE+PF的值为点P相对于∠MON的“点角距离”,记为d(P,∠MON).如图乙,在平面直角坐标系xOy中,点P在第一象限内,且点P的横坐标比纵坐标大1,对于∠xOy,满足d(P,∠xOy)=5,点P的坐标是(3,2).
分析 设点P的横坐标为x,表示出纵坐标,然后列方程求出x,再求解即可.
解答 解:设点P的横坐标为x,则点P的纵坐标为x-1,
由题意得,x+x-1=5,
解得x=3,
x-1=2,
所以,点P(3,2).
故答案为:(3,2).
点评 本题考查了点的坐标,读懂题目信息,理解“点角距离”的定义并列出方程是解题的关键.

练习册系列答案
相关题目
5.若反比例函数y=$\frac{k}{x}$的图象经过点(-$\frac{3}{2}$,2),则这个函数的图象一定经过点( )
| A. | (-$\frac{2}{3}$,3) | B. | (-$\frac{3}{2}$,-2) | C. | (3,-1) | D. | (-2,-$\frac{3}{2}$) |
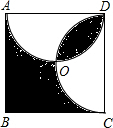 如图,分别以正方形ABCD的边AD和DC为直径画两个半圆交于点O,若正方形的边长为10cm,求阴影部分的面积.
如图,分别以正方形ABCD的边AD和DC为直径画两个半圆交于点O,若正方形的边长为10cm,求阴影部分的面积.