��Ŀ����
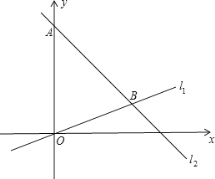
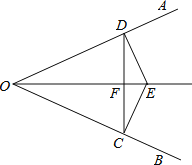
����Ŀ����ֱ֪��l1��l2 �� ��A��l1�ϵĶ��㣬��B��l1�ϣ���C��D��l2�ϣ���ABC����ADC��ƽ���߽��ڵ�E�������B��D�غϣ���
��1������A�ڵ�B����࣬��ABC=80�㣬��ADC=60�㣬����E��EF��l1 �� ��ͼ����ʾ�����BED�Ķ����� 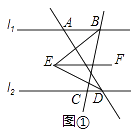
��2������A�ڵ�B����࣬��ABC=���㣬��ADC=60�㣬��ͼ����ʾ�����BED�Ķ�������ֱ��д������Ľ���� 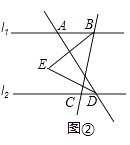
��3������A�ڵ�B���Ҳ࣬��ABC=���㣬��ADC=60�㣬��ͼ����ʾ�����BED�Ķ����� 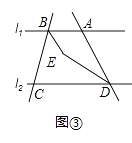
���𰸡�
��1���⣺��BE��DE�ֱ��ǡ�ABC����ADC��ƽ���ߣ�
���ABE= ![]() ��ABC=
��ABC= ![]() ��80��=40�㣬��CDE=
��80��=40�㣬��CDE= ![]() ��ADC=
��ADC= ![]() ��60��=30�㣮
��60��=30�㣮
��EF��L1��
���BEF=��ABE=40�㣮
��L1��L2
��EF��L2
���DEF=��CDE=30��
���BED=��BEF+��DEF=40��+30��=70��
��2���⣺BE��DE�ֱ��ǡ�ABC����ADC��ƽ���ߣ�
���ABE= ![]() ��ABC=
��ABC= ![]() ���㣬��CDE=
���㣬��CDE= ![]() ��ADC=
��ADC= ![]() ��60��=30�㣮
��60��=30�㣮
��EF��L1��
���BEF=��ABE= ![]() ���㣮
���㣮
��L1��L2��
��EF��L2��
���DEF=��CDE=30��
���BED=��BEF+��DEF= ![]() ����+30�㣬����BED=��
����+30�㣬����BED=�� ![]() ��+30����
��+30����
��3���⣺����E��EF��L1��
��BE��DE�ֱ��ǡ�ABC����ADCƽ���ߣ�
���ABE= ![]() ��ABC=
��ABC= ![]() ���㣬��CDE=
���㣬��CDE= ![]() ��ADC=
��ADC= ![]() ��60��=30�㣮
��60��=30�㣮
��EF��L1��
���BEF=��180�� ![]() �����㣮
�����㣮
�֡�L1��L2
��EF��L2
���DEF=��CDE=30��
���BED=��BEF+��DEF
=��180�� ![]() ��+30����
��+30����
=��210�� ![]() ������
������
����������1������BE��DE�ֱ��ǡ�ABC����ADC��ƽ���ߣ��ó���ABE= ![]() ��ABC����CDE=
��ABC����CDE= ![]() ��ADC������ƽ���ߵ����ʵó���BEF=��ABE��ͬ���ɵó���DEF=��CDE�����ɡ�BED=��BEF+��DEF���ɵó����ۣ���2������E��EF��AB��ͬ��1����֤��������ȫ��ͬ����3������E��EF��L1 �� ����BE��DE�ֱ��ǡ�ABC����ADCƽ���߿�֪��ABE=
��ADC������ƽ���ߵ����ʵó���BEF=��ABE��ͬ���ɵó���DEF=��CDE�����ɡ�BED=��BEF+��DEF���ɵó����ۣ���2������E��EF��AB��ͬ��1����֤��������ȫ��ͬ����3������E��EF��L1 �� ����BE��DE�ֱ��ǡ�ABC����ADCƽ���߿�֪��ABE= ![]() ��ABC=
��ABC= ![]() ���㣬��CDE=
���㣬��CDE= ![]() ��ADC������EF��L1��֪��BEF=��180��
��ADC������EF��L1��֪��BEF=��180�� ![]() �����㣮����L1��L2��֪EF��L2 �� �ʡ�DEF=��CDE=30�㣬���ԡ�BED=��BEF+��DEF��
�����㣮����L1��L2��֪EF��L2 �� �ʡ�DEF=��CDE=30�㣬���ԡ�BED=��BEF+��DEF��
�����㾫����������Ҫ������ƽ���ߵ����ʵ����֪ʶ�㣬��Ҫ������ֱ��ƽ�У�ͬλ����ȣ���ֱ��ƽ�У��ڴ�����ȣ���ֱ��ƽ�У�ͬ���ڽǻ���������ȷ�����⣮