Question

已知矩形ABCD的边AB=4，AD=3，现将矩形ABCD如图放在直线l上，且沿着l向右作无滑动地翻滚，当它翻滚到位置A₁B₁C₁D₁时，计算：

（1）顶点A所经过的路线长为______；
（2）点A经过的路线与直线l所围成的面积为______．

Answer 1

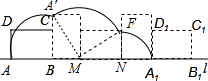解：（1）如图所示：
∵AB=4，AD=3，
∴A′M==5，
顶点A所经过的路线长为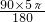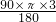：++=6π；

（2）点A经过的路线与直线l所围成的面积为：
S_扇形ABA′+S_△A′BM+S_扇形A′MF+S_△MFN+
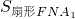
=+×4×3++×4×3+，
=π+12．
故答案为：6π；π+12．
分析：（1）根据图形的滚动路线得出顶点A所经过的路线长为3段扇形弧长进而求出即可；
（2）根据图形得出点A经过的路线与直线l所围成的面积为S_扇形ABA′+S_△A′BM+S_扇形A′MF+S_△MFN+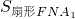求出即可．
点评：此题主要考查了图形的旋转以及扇形弧长公式和扇形面积公式应用，根据已知得出滚动路线是解题关键．