题目内容
如图,已知CD是⊙O的直径,AC⊥CD,垂足为C,弦DE∥OA,直线AE、CD相交于点B.

1.求证:直线AB是⊙O的切线
2.当AC=1,BE=2,求tan∠OAC的值.
1.证明:如图,连接OE,

∵弦DE∥OA,∴∠COA=∠ODE, ∠EOA=∠OED, ∵OD=OE,
∴∠ODE=∠OED, ∴∠COA=∠EOA,又∵OC=OE,OA=OA,∴⊿OAC≌⊿OAE,
∴∠OEA=∠OCA=90°, ∴OE⊥AB,∴直线AB是OO的切线
(1) 2.由(1)知⊿OAC≌⊿OAE, ∴AE=AC=1,AB=1+2=3,在直角⊿ABC中,
![]() ,∵∠B=∠B, ∠BCA=∠BOE,∴⊿BOE∽⊿BAC,
,∵∠B=∠B, ∠BCA=∠BOE,∴⊿BOE∽⊿BAC,
∴![]() ,∴在直角⊿AOC中,tan∠OAC=
,∴在直角⊿AOC中,tan∠OAC=![]() .
.
解析:略

练习册系列答案
相关题目
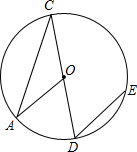 如图,已知CD是⊙O的直径,过点D的弦DE平行于半径OA,若∠D的度数是50°,则∠C的度数是( )
如图,已知CD是⊙O的直径,过点D的弦DE平行于半径OA,若∠D的度数是50°,则∠C的度数是( )| A、25° | B、30° | C、40° | D、50° |
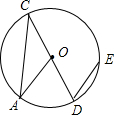 如图,已知CD是⊙O的直径,弦DE∥半径OA,∠D=50°,∠C=( )
如图,已知CD是⊙O的直径,弦DE∥半径OA,∠D=50°,∠C=( )| A、50° | B、40° | C、25° | D、20° |
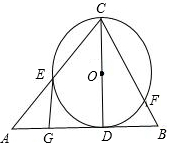 如图,已知CD是△ABC中AB边上的高,以CD为直径的⊙O交CA于点E,点G是AD的中点.
如图,已知CD是△ABC中AB边上的高,以CD为直径的⊙O交CA于点E,点G是AD的中点.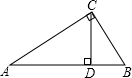 如图,已知CD是Rt△ABC的斜边上的高,其中AD=9cm,BD=4cm,那么CD等于
如图,已知CD是Rt△ABC的斜边上的高,其中AD=9cm,BD=4cm,那么CD等于 (2012•苍梧县二模)如图,已知CD是⊙O的直径,AC⊥CD,垂足为C,弦DE∥OA,直线AE,CD相交于点B.
(2012•苍梧县二模)如图,已知CD是⊙O的直径,AC⊥CD,垂足为C,弦DE∥OA,直线AE,CD相交于点B.