题目内容
化简,求值.
(1)先化简,再求值:(x+3)(x-3)-x(x-2),其中x=4;
(2)先化简,再求值:(2a-b)2-b2,其中a=2,b=3;
(3)已知210=a2=4b,化简 ,并求值.
,并求值.
解:(1)(x+3)(x-3)-x(x-2)
=x2-9-x2+2x
=2x-9,
把x=4代入原式得:原式=2×4-9=-1;
(2)(2a-b)2-b2
=4a2-4ab+b2-b2
=4a2-4ab,
把a=2,b=3代入原式得:原式=4×22-4×2×3=4×4-24=-8;
(3)∵210=a2,
∴(25)2=a2,
∴a=±32,
∵210=4b,
∴(25)2=45=4b,
∴b=5,
∵
=( a)2-(
a)2-( b)2-(
b)2-( a)2-(
a)2-( b)2-2×
b)2-2× a×
a× b
b
=- ab-
ab-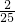 b2,
b2,
∴原式=- ab-
ab-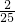 b2=-
b2=- ×32×5-
×32×5-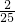 ×52=-18或=-
×52=-18或=- ×(-32)×5-
×(-32)×5-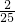 ×52=14.
×52=14.
分析:(1)根据平方差公式进行计算,再合并同类项,然后把x的值代入即可;
(2)根据完全平方公式把要求的式子进行整理,再把a,b的值代入即可;
(3)根据210=a2=4b,求出a,b的值,再把要求的式子根据平方差公式和完全平方公式进行整理,再把a,b的值代入即可得出答案.
点评:此题考查了整式的混合运算-化简求值,关键是把要求的式子化到最简,再代值进行计算,在计算时要注意结果的符号.
=x2-9-x2+2x
=2x-9,
把x=4代入原式得:原式=2×4-9=-1;
(2)(2a-b)2-b2
=4a2-4ab+b2-b2
=4a2-4ab,
把a=2,b=3代入原式得:原式=4×22-4×2×3=4×4-24=-8;
(3)∵210=a2,
∴(25)2=a2,
∴a=±32,
∵210=4b,
∴(25)2=45=4b,
∴b=5,
∵

=(
 a)2-(
a)2-( b)2-(
b)2-( a)2-(
a)2-( b)2-2×
b)2-2× a×
a× b
b=-
 ab-
ab-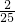 b2,
b2,∴原式=-
 ab-
ab-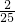 b2=-
b2=- ×32×5-
×32×5-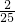 ×52=-18或=-
×52=-18或=- ×(-32)×5-
×(-32)×5-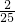 ×52=14.
×52=14.分析:(1)根据平方差公式进行计算,再合并同类项,然后把x的值代入即可;
(2)根据完全平方公式把要求的式子进行整理,再把a,b的值代入即可;
(3)根据210=a2=4b,求出a,b的值,再把要求的式子根据平方差公式和完全平方公式进行整理,再把a,b的值代入即可得出答案.
点评:此题考查了整式的混合运算-化简求值,关键是把要求的式子化到最简,再代值进行计算,在计算时要注意结果的符号.

练习册系列答案
相关题目