题目内容
已知1=12,1+3=22,1+3+5=32,1+3+5+7=42,1+3+5+7+9=52,…根据前面各式的规律可猜测:1+3+5+7+…+(2n-1)=______.
从1+3=4=22,1+3+5=9=32,1+3+5+7=16=42,三个等式中,可以看出等式左边最后一个数+1再除以2即得到等式右边幂的底数,
2=
,3=
,4=
,从而得
=n,
即:1+3+5+7+…+(2n-1)=n2.
故答案为:n2.
2=
| 3+1 |
| 2 |
| 5+1 |
| 2 |
| 7+1 |
| 2 |
| 2n-1+1 |
| 2 |
即:1+3+5+7+…+(2n-1)=n2.
故答案为:n2.

练习册系列答案
相关题目
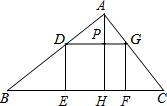 如图,矩形DEFG的边EF在△ABC的边BC上,顶点D、G分别在边AB、AC上,AH⊥BC,垂足为H.已知BC=12,AH=8.当矩形DEFG面积最大时,求矩形的长和宽.
如图,矩形DEFG的边EF在△ABC的边BC上,顶点D、G分别在边AB、AC上,AH⊥BC,垂足为H.已知BC=12,AH=8.当矩形DEFG面积最大时,求矩形的长和宽.