��Ŀ����
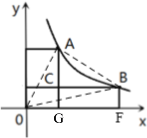
����Ŀ����֪��A��B�ڷ���������![]() (x>0)��ͼ���ϣ����ǵĺ�����ֱ�Ϊm��n����m��n������A����B����x�ᣬy�������߶Σ������������߶εĽ���ΪC��
(x>0)��ͼ���ϣ����ǵĺ�����ֱ�Ϊm��n����m��n������A����B����x�ᣬy�������߶Σ������������߶εĽ���ΪC��

��1����ͼ����m=2��n=6ʱ��ֱ��д����C�����꣺
��2����A(m��n)��B(n��m)������OA��OB��AB������AOB�������(�ú�m�Ĵ���ʽ��ʾ)
��3����AD��y���ڵ�D��BE��x���ڵ�E����![]() ����
����![]() ����C��ֱ��DE��ʱ����p��ȡֵ��Χ��
����C��ֱ��DE��ʱ����p��ȡֵ��Χ��
���𰸡���1����C����Ϊ��2��1������2��S��AOB=![]() ��0��m��
��0��m��![]() ������3��
������3��![]() ��p��
��p��![]() ��
��
��������
��1����n=6���뷴������������ʽ�������B���꣬���ɵô𰸣�
��2����ͼ���ɷ���������k�ļ�������ɵ�S��AOG=S��BOF�������ɵ�S��AOB=S�ı���AGFB���������������ʽ���ɵô𰸣�
��3����ͼ����A��B�������m��n��ʾ����C��E��D���꣬���ô���ϵ�����ɵó�DE����ʽ����C���������ɵ�m��n�Ĺ�ϵ������![]() ����n��ʾ��p������n��ȡֵ��Χ�����ò���ʽ�����ʼ��ɵô𰸣�
����n��ʾ��p������n��ȡֵ��Χ�����ò���ʽ�����ʼ��ɵô𰸣�
��1����n=6����B��![]() (x>0)��ͼ���ϣ����ĺ�����ֱ�Ϊn��
(x>0)��ͼ���ϣ����ĺ�����ֱ�Ϊn��
��y=![]() =1��
=1��
��B��6��1����
��m=2���������߶εĽ���ΪC��
���C������2��1����
��2����ͼ��
�ߵ�A��B�ڷ���������![]() (x>0)��ͼ���ϣ�
(x>0)��ͼ���ϣ�
��S��AOG=S��BOF=![]() ��6=3��
��6=3��
��S��AOB=S��AOG+S�ı���AGFB-S��BOF=S�ı���AGFB��
��A(m��n)��B(n��m)��
��AG=n��OG=m��OF=n��BF=m��n=![]() ��
��
�ߵ�B�ڵ�A�Ҳ࣬m��n��m��0��n��0��
��0��m��![]() ��
��
��S��AOB=![]() (m+n)(n-m)=
(m+n)(n-m)=![]() (n2-m2)=
(n2-m2)=![]() ��0��m��
��0��m��![]() ����
����
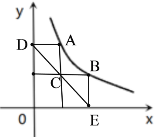
��3����ͼ��
�ߵ�A��B��![]() (x>0)��ͼ���ϣ����ǵĺ�����ֱ�Ϊm��n��
(x>0)��ͼ���ϣ����ǵĺ�����ֱ�Ϊm��n��
��A��m��![]() ����B��n��
����B��n��![]() ����m��0��n��0����
����m��0��n��0����
��C��m��![]() ����E��n��0����D��0��
����E��n��0����D��0��![]() ����
����
��ֱ��DE�Ľ���ʽΪy=kx+b��
��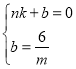 ��
��
��ã�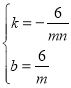 ��
��
��ֱ��DE�Ľ���ʽΪy=![]() ��
��
�ߵ�C��ֱ��DE�ϣ�
��![]() ��
��
�����ã�m=![]() n��
n��
��![]() =1-
=1-![]() ��
��
��![]() ��
��
��2��2n��8��
��![]() ��
��![]() ��
��![]() ��
��
��![]() ��1-
��1-![]() ��
��![]() ��
��
��p��ȡֵ��ΧΪ![]() ��p��
��p��![]() ��
��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�