Question

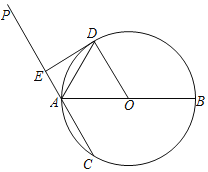
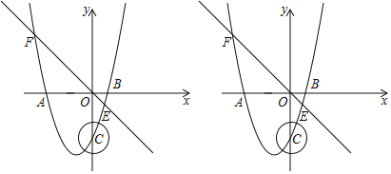
【题目】如图，半径为5的⊙O与y轴相交于A点，B为⊙O在x轴上方的一个动点（不与点A重合），C为y轴上一点且∠OCB＝60°，I为△BCO的内心，则△AIO的外接圆的半径的取值（或取值范围）为_____．

Answer 1

【答案】

【解析】

首先证明∠AIO＝120°＝定值，OA＝5＝定值，推出点G的运动轨迹是，推出△AOI的外接圆的半径是定值，由此即可解决问题．

如图，

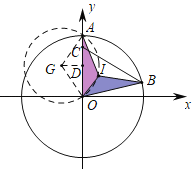
∵∠BCO＝60°，

∴∠CBO+∠COB＝120°，

∵I是内心，

∴∠IOB＝∠COB，∠IBO＝∠CBO，

∴∠IOB+∠IBO＝(∠COB+CBO)＝60°，

∴∠OIB＝180°﹣∠IOB﹣∠IBO＝120°，

∵OA＝OB，∠AOI＝∠BOI，OI＝OI，

∴△AIO≌△BOI（SAS），

∴∠AIO＝∠BIO＝120°，

作△AOI的外接圆⊙G，连接AG，OG，作GD⊥OA于D．

∵∠AIO＝120°＝定值，OA＝5＝定值，

∴点G的运动轨迹是，

∴△AOI的外接圆的半径是定值，

∵GA＝GO，GD⊥OA，∠AGO＝120°，

∴∠AGD＝∠AGO＝120°，AD＝OD＝，

∴AG＝＝＝．

故答案为．