题目内容
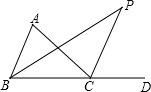 如图,△ABC一内角和外角角平分线相交于点P,已知∠A的度数为α,则∠BPC的度数是
如图,△ABC一内角和外角角平分线相交于点P,已知∠A的度数为α,则∠BPC的度数是| 1 |
| 2 |
| 1 |
| 2 |
分析:根据BP为∠ABC的角平分线,CP为△ABC外角∠ACD的平分线,可知,∠A=180°-∠1-∠3,∠P=180°-∠4=∠5=180°-∠3-
(∠A+2∠1),两式联立可得2∠P=∠A.
| 1 |
| 2 |
解答: 解:∵BP为∠ABC的内角平分线,CP为△ABC外角∠ACD的平分线,两角平分线交于点P,
解:∵BP为∠ABC的内角平分线,CP为△ABC外角∠ACD的平分线,两角平分线交于点P,
∴∠1=∠2,∠5=
(∠A+2∠1),∠3=∠4,
在△ABE中,∠A=180°-∠1-∠3
∴∠1+∠3=180°-∠A----①
在△CPE中,∠P=180°-∠4-∠5=180°-∠3-
(∠A+2∠1),
即2∠P=360°-2∠3-∠A-2∠1=360°-2(∠1+∠3)-∠A----②,
把①代入②得2∠P=∠A,即∠BPC=
α.
故答案为:
α.
 解:∵BP为∠ABC的内角平分线,CP为△ABC外角∠ACD的平分线,两角平分线交于点P,
解:∵BP为∠ABC的内角平分线,CP为△ABC外角∠ACD的平分线,两角平分线交于点P,∴∠1=∠2,∠5=
| 1 |
| 2 |
在△ABE中,∠A=180°-∠1-∠3
∴∠1+∠3=180°-∠A----①
在△CPE中,∠P=180°-∠4-∠5=180°-∠3-
| 1 |
| 2 |
即2∠P=360°-2∠3-∠A-2∠1=360°-2(∠1+∠3)-∠A----②,
把①代入②得2∠P=∠A,即∠BPC=
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查的是三角形内角和定理,熟知三角形的内角和等于180°是解答此题的关键.

练习册系列答案
相关题目
 24、(1)如图,△ABC纸片中,∠A=36°,AB=AC,请你剪两刀,分成3张小纸片,使每张小纸片都是等腰三角形.请画出示意图,并标明必要的角度;
24、(1)如图,△ABC纸片中,∠A=36°,AB=AC,请你剪两刀,分成3张小纸片,使每张小纸片都是等腰三角形.请画出示意图,并标明必要的角度;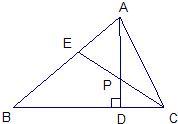 21、如图,△ABC中AD是BC边上的高,CE是△ABC的一条角平分线,它们相交于点P.已知∠APE=55°,∠AEP=75°,求△ABC的各个内角的度数.
21、如图,△ABC中AD是BC边上的高,CE是△ABC的一条角平分线,它们相交于点P.已知∠APE=55°,∠AEP=75°,求△ABC的各个内角的度数.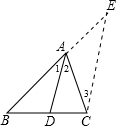 E∥AD,交BA的延长线于E,从而得到BD、DC、AB的第四比例项AE,这样,证明
E∥AD,交BA的延长线于E,从而得到BD、DC、AB的第四比例项AE,这样,证明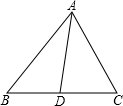 []
[] 学习了勾股定理的逆定理,我们知道:在一个三角形中,如果两边的平方和等于第三边的平方,那么这个三角形为直角三角形.类似地,我们定义:对于任意的三角形,设其三个角的度数分别为x°、y°和z°,若满足x2+y2=z2,则称这个三角形为勾股三角形.
学习了勾股定理的逆定理,我们知道:在一个三角形中,如果两边的平方和等于第三边的平方,那么这个三角形为直角三角形.类似地,我们定义:对于任意的三角形,设其三个角的度数分别为x°、y°和z°,若满足x2+y2=z2,则称这个三角形为勾股三角形.