题目内容
(1997•江西)下列方程:
(1)(
)2-5(
)+6=0,
(2)x2+x+1=
,
(3)
+
=
,
(4)3x2+15x+2
=2,
其中可以用换元法来解的方程的个数有( )
(1)(
| x |
| x-1 |
| x |
| x-1 |
(2)x2+x+1=
| 2 |
| x2+x |
(3)
|
|
| 5 |
| 2 |
(4)3x2+15x+2
| x2+5x+1 |
其中可以用换元法来解的方程的个数有( )
分析:(1)设y=
,方程换元得到关于y的方程;
(2)设y=x2+x,方程换元得到关于y的方程;
(3)设y=
,方程换为关于y的方程;
(4)设y=
,方程换元为关于y的方程.
| x |
| x-1 |
(2)设y=x2+x,方程换元得到关于y的方程;
(3)设y=
|
(4)设y=
| x2+5x |
解答:解:(1)设y=
,方程换元得到关于y的方程y2-5y+6=0;
(2)设y=x2+x,方程换元得到关于y的方程y+1=
;
(3)设y=
,方程换为关于y的方程y+
=
;
(4)设y=
,方程换元为关于y的方程3y2+2y=2.
则可以用换元法来解的方程的个数有4个.
故选D.
| x |
| x-1 |
(2)设y=x2+x,方程换元得到关于y的方程y+1=
| 2 |
| y |
(3)设y=
|
| 1 |
| y |
| 5 |
| 2 |
(4)设y=
| x2+5x |
则可以用换元法来解的方程的个数有4个.
故选D.
点评:此题考查了换元法解分式方程,以及无理方程,用换元法解一些复杂的分式方程是比较简单的一种方法,根据方程特点设出相应未知数,解方程能够使问题简单化,注意求出方程解后要验根.

练习册系列答案
相关题目
 (1997•江西)已知:如图,AB=AC,∠A=36°,AB的垂直平分线交AC于D,则下列结论:
(1997•江西)已知:如图,AB=AC,∠A=36°,AB的垂直平分线交AC于D,则下列结论: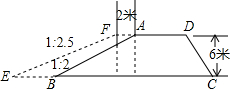 (1997•江西)如图,沿水库拦水坝的背水坡将坝顶加宽2米,坡度由原来的1:2改成1:2.5.已知坝高6米,坝长50米.
(1997•江西)如图,沿水库拦水坝的背水坡将坝顶加宽2米,坡度由原来的1:2改成1:2.5.已知坝高6米,坝长50米.