Question

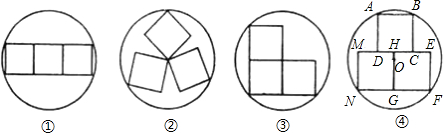
用四个边长均为a、b、c的直角三角板，拼成如图中所示的图形，则下列结论中正确的是（　　）

• A、c²=a²+b²
• B、c²=a²+2ab+b²
• C、c²=a²-2ab+b²
• D、c²=（a+b）²．

Answer 1

分析：四个一样的直角三角板围成的四边形为正方形，其中小四边形也为正方形，大正方形的面积可以由边长的平方求出，也可以由四个直角三角形的面积与小正方形面积之和来求，两种方法得出的面积相等，利用完全平方公式展开，合并后即可得到正确的等式．

解答：解：由题意得到四个完全一样的直角三角板围成的四边形为正方形，其边长为c，
里边的小四边形也为正方形，边长为b-a，
则有c²=

1

2

ab×4+（b-a）²，
整理得：c²=a²+b²．
故选A．

点评：此题考查了整式的混合运算，根据题意列出相应的等式是解本题的关键．