Question

【题目】如图1，抛物线与轴相交于、两点（点在点的右侧），与轴相交于点，对称轴与轴相交于点，与相交于点．

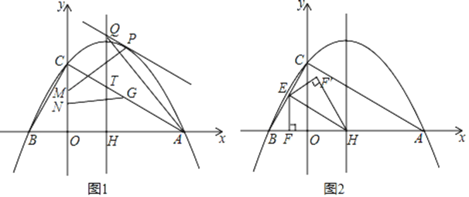
（1）点是线段上方抛物线上一点，过点作交抛物线的对称轴于点，当面积最大时，点、在轴上（点在点的上方），，点在直线上，求的最小值．

（2）点为中点，轴于，连接，将沿翻折得△，如图所示，再将△沿直线平移，记平移中的△为△，在平移过程中，直线与轴交于点，则是否存在这样的点，使得△为等腰三角形？若存在，求出点坐标．

Answer 1

【答案】（1）的最小值为；（2）点的坐标为或．

【解析】

（1）由抛物线解析式可求A(6，0)，C(0，)，对称轴x=2，过P点作PT′∥QT，由PQ∥AC可知，四边形QTT′P是平行四边形，QT=PT’，因为HT为定值，所以PT′最大时，△AQH面积最大，由此构建二次函数，求出点P坐标，过点G作GE⊥x轴于E，作x轴关于直线AC的对称直线l，E的对称点为E′，将PM沿y轴向下平移个单位至P′N，作点P′关于y轴的对称点P″，过P″作P″S⊥l于S，则有PM+NG+GA=P″N+NG+GE′≥P″S，求出P″S即可；
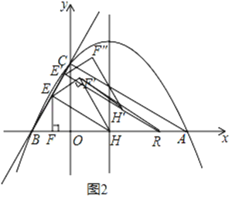
（2）先求得点E，F，F′，H′，R的坐标，根据△RF'H'为等腰三角形，分三种情况分别求解即可．

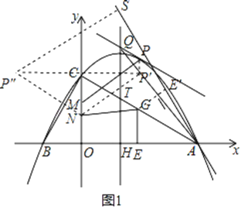
（1）如图1，抛物线与轴相交于、两点（点在点的右侧），

；；，，

直线的解析式为：，

，

过点作，交于，

设，，

则

，

四边形是平行四边形，

，

当面积最大时，最大，即最大，

即时，面积最大，

此时点坐标为．

过点作轴于，作轴关于直线的对称直线，的对称点为，将沿轴向下平移个单位至，作点关于轴的对称点，过作于，则有

，与关于轴对称

，

，直线与轴关于直线对称

，

设直线的解析式为，则

，将代入得：，解得：，

直线的解析式为，

过点作轴交于，则，，

，

轴

，

的最小值；

（2）

抛物线对称轴为直线，

，

由（1）知：；；，，

点为中点，轴于，

，

，

△沿直线平移，各个点横纵坐标变化为，设△沿直线平移后的△各顶点坐标分别为

，

则直线解析式为，令，则

，

，

，

，

△为等腰三角形，

或或，

①当时，则，解得：，

此时，或

②当时，则，解得：或，

不符合题意，与①重复

③当时，，解得：，与①重复

综上所述，点的坐标为或．