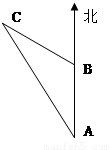题目内容
 如图,上午8时,一艘船从A处出发,以15海里/时的速度向正北方向航行,9时40分到达B处,从A处测得灯塔C在北偏西26°方向,从B处测得灯塔C在北偏西52°方向,则B处到灯塔C的距离是
如图,上午8时,一艘船从A处出发,以15海里/时的速度向正北方向航行,9时40分到达B处,从A处测得灯塔C在北偏西26°方向,从B处测得灯塔C在北偏西52°方向,则B处到灯塔C的距离是
- A.36海里
- B.25海里
- C.20海里
- D.21海里
B
分析:根据所给的角的度数,容易证得△BCA是等腰三角形,而AB的长易求,所以根据等腰三角形的性质,BC的值也可以求出.
解答:据题意得,∠A=26°,∠DBC=52°,
∵∠DBC=∠A+∠C,
∴∠A=∠C=26°,
∴AB=BC,
∵AB=15× =25,
=25,
∴BC=25(海里).
故选B.
点评:本题考查了等腰三角形的性质及方向角的问题;由已知得到三角形是等腰三角形是正确解答本题的关键.要学会把实际问题转化为数学问题,用数学知识进行解决实际问题的方法.
分析:根据所给的角的度数,容易证得△BCA是等腰三角形,而AB的长易求,所以根据等腰三角形的性质,BC的值也可以求出.
解答:据题意得,∠A=26°,∠DBC=52°,
∵∠DBC=∠A+∠C,
∴∠A=∠C=26°,
∴AB=BC,
∵AB=15×
 =25,
=25,∴BC=25(海里).
故选B.
点评:本题考查了等腰三角形的性质及方向角的问题;由已知得到三角形是等腰三角形是正确解答本题的关键.要学会把实际问题转化为数学问题,用数学知识进行解决实际问题的方法.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
 23、如图,上午8时,一艘轮船从A处向正北方向航行,每小时航行15海里,11时轮船到达B处,从A、B处望小岛P,测得∠PAC=15°,∠PBC=30°,求从B处到小岛P的距离.
23、如图,上午8时,一艘轮船从A处向正北方向航行,每小时航行15海里,11时轮船到达B处,从A、B处望小岛P,测得∠PAC=15°,∠PBC=30°,求从B处到小岛P的距离. 如图,上午8时,一艘船从A处出发,以15海里/时的速度向正北方向航行,9时40分到达B处,从A处测得灯塔C在北偏西26°方向,从B处测得灯塔C在北偏西52°方向,则B处到灯塔C的距离是( )
如图,上午8时,一艘船从A处出发,以15海里/时的速度向正北方向航行,9时40分到达B处,从A处测得灯塔C在北偏西26°方向,从B处测得灯塔C在北偏西52°方向,则B处到灯塔C的距离是( )