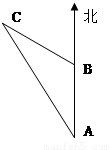题目内容
23、如图，上午8时，一艘轮船从A处向正北方向航行，每小时航行15海里，11时轮船到达B处，从A、B处望小岛P，测得∠PAC=15°，∠PBC=30°，求从B处到小岛P的距离．分析：先根据三角形外角的性质及∠PAC=15°，∠PBC=30°，求出△ABP是等腰三角形，再根据等腰三角形的性质即可解答．
解答：解：∵∠PBC是△PAB的外角，
∴∠PBC=∠PAC+∠APB，
又∵∠PAC=15°，∠PBC=30°，
∴∠APB=15°，
∴∠APB=∠PAC，
∴AB=BP，
又∵AB=15×3=45海里，
∴BP=45海里，即从B处到小岛P的距离为45海里．
∴∠PBC=∠PAC+∠APB，
又∵∠PAC=15°，∠PBC=30°，
∴∠APB=15°，
∴∠APB=∠PAC，
∴AB=BP，
又∵AB=15×3=45海里，
∴BP=45海里，即从B处到小岛P的距离为45海里．
点评：此题比较简单，根据三角形外角的性质求出△ABP是等腰三角形是解答此题的关键．
练习册系列答案
相关题目
如图，上午8时，一艘船从A处出发，以15海里/时的速度向正北方向航行，9时40分到达B处，从A处测得灯塔C在北偏西26°方向，从B处测得灯塔C在北偏西52°方向，则B处到灯塔C的距离是（ ）
