题目内容
等边三角形ABC的三条角平分线AD、BE、CF交于点O，则OD：OA=________．
1：2
分析：根据等腰三角形三线合一的性质解答．
解答：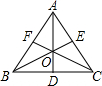
解：如下图所示：
∵△ABC是等边三角形，AD、BE、CF为三条角平分线，
∴AD、BE、CF为三条高，
∴∠OAE=∠OCD=∠OCE=30°，CD=CE=
AB．
∵CO=CO，
∴△OCD≌△OCE．（SAS）
∴OE=OD．
∵在Rt△OEA中，
sin∠OAE=
=，
∴OD：OA=1：2．
故答案为：1：2．
点评：此题考查了等腰三角形的性质及特殊角的三角函数值．
分析：根据等腰三角形三线合一的性质解答．
解答：
解：如下图所示：∵△ABC是等边三角形，AD、BE、CF为三条角平分线，
∴AD、BE、CF为三条高，
∴∠OAE=∠OCD=∠OCE=30°，CD=CE=
AB．∵CO=CO，
∴△OCD≌△OCE．（SAS）
∴OE=OD．
∵在Rt△OEA中，
sin∠OAE=
=，∴OD：OA=1：2．
故答案为：1：2．
点评：此题考查了等腰三角形的性质及特殊角的三角函数值．
练习册系列答案
相关题目
19、如图，已知三个同心圆，等边三角形ABC的三个项点分别在三个圆上，请你先把这个三角形绕着点O顺时针旋转120°，再说明旋转的结果．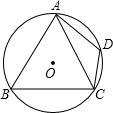
如图，等边三角形ABC的三个顶点都在⊙O上，D是
已知：如图，在等边三角形ABC的三边上，分别取点D，E，F使AD=BE=CF．
如图，等边三角形ABC的三条中线交于点O，则图中除△ABC外，还有