题目内容
5.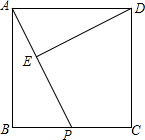 如图,正方形ABCD中,AB=4$\sqrt{5}$,P是BC的中点,DE⊥AP,垂足为点E.
如图,正方形ABCD中,AB=4$\sqrt{5}$,P是BC的中点,DE⊥AP,垂足为点E.(1)求AP的长.
(2)将△ADE沿着射线AP平移,设点A平移的距离为x,平移后的图形与四边形APCD重叠的面积为y,求y与x的函数关系,并直接写出x的取值范围.
分析 (1)根据题意,可得AB=4$\sqrt{5}$,BP=4$\sqrt{5}$$÷2=2\sqrt{5}$;然后在直角三角形ABP中,根据勾股定理,求出AP的长是多少即可;
(2)首先根据相似三角形的判定方法,判断出△ABP∽△DEA,求出EA、E′A′、DE、D′E′的值是多少,进而求出三角形A′D′E′的面积是多少;然后判断出△DD′G∽△D′E′A′,△D′FG∽△D′E′A′,进而求出FG、D′F的大小,再用三角形A′D′E′的面积减去三角形FGD′的面积,求出y的值是多少,判断出y与x的函数关系,再根据AP的长度判断出x的取值范围即可.
解答 解:(1)因为AB=4$\sqrt{5}$,BP=4$\sqrt{5}$$÷2=2\sqrt{5}$,
所以AP=$\sqrt{{AB}^{2}{+BP}^{2}}=\sqrt{{(4\sqrt{5})}^{2}{+(2\sqrt{5})}^{2}}$=$\sqrt{80+20}=10$;
(2)如图: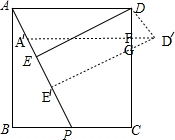 ,
,
∵DE⊥AP,∴∠DAE+∠ADE=90°,
∵∠DAE+∠BAP=90°,∴∠ADE=∠BAP,∠ABP=∠DEA,
∴△ABP∽△DEA,$\frac{EA}{BP}=\frac{DA}{AP}$,
∴EA=4$\sqrt{5}×2\sqrt{5}$÷10=4,A′E′=4,
∴DE=$\sqrt{{AD}^{2}{-AE}^{2}}$=$\sqrt{{(4\sqrt{5})}^{2}{-4}^{2}}$=$\sqrt{80-16}$=8,D′E′=8,
∴三角形A′D′E′的面积是:4×8÷2=16,
∵△DD′G∽△D′E′A′,
∴$\frac{DD′}{D′E′}=\frac{D′G}{E′A′}=\frac{D′G}{4}$,∴D′G=4x÷8=0.5x,
∵△D′FG∽△D′E′A′,
∴$\frac{D′F}{D′E′}=\frac{FG}{E′A′}=\frac{FG}{4}$,D′F=8FG÷4=2FG,
∴FG2+(2FG)2=(0.5x)2,
解得FG=$\frac{\sqrt{5}}{10}x$,
∴D′F=$\frac{\sqrt{5}}{10}x×2=\frac{\sqrt{5}}{5}x$,
∵0<x≤AP,
∴y=16-$(\frac{\sqrt{5}}{10}x)×(\frac{\sqrt{5}}{5}x)×\frac{1}{2}$=16-$\frac{{x}^{2}}{20}$(0<x≤10).
点评 此题主要考查了正方形的性质,平移的性质,以及相似三角形的判定和三角形的面积的求法,要熟练掌握.

 名校通行证有效作业系列答案
名校通行证有效作业系列答案| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
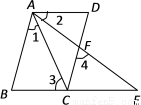

 B.
B.  C.
C.  D.
D. 
 的结果是( )
的结果是( ) B.
B.  C.
C.  D. 2(x+1)
D. 2(x+1)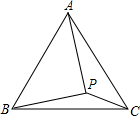 如图,在等边△ABC内有一点P,且PA=2,PB=$\sqrt{3}$,PC=1.
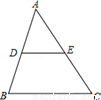
如图,在等边△ABC内有一点P,且PA=2,PB=$\sqrt{3}$,PC=1.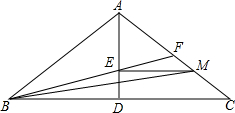 如图,在等腰三角形ABC中,AD⊥BC于点D,AD=3,DC=4,点M在线段AC上运动,ME⊥AD于点E,连结BE并延长交AC于点F,连结BM.设$\frac{CM}{AC}$=m(0<m<1),△BEM的面积为S.
如图,在等腰三角形ABC中,AD⊥BC于点D,AD=3,DC=4,点M在线段AC上运动,ME⊥AD于点E,连结BE并延长交AC于点F,连结BM.设$\frac{CM}{AC}$=m(0<m<1),△BEM的面积为S.