Question

【题目】△CDE和△AOB是两个等腰直角三角形，∠CDE＝∠AOB＝90°，DC＝DE＝1，OA＝OB＝a（a＞1）．

（1）将△CDE的顶点D与点O重合，连接AE，BC，取线段BC的中点M，连接OM．

①如图1，若CD，DE分别与OA，OB边重合，则线段OM与AE有怎样的数量关系？请直接写出你的结果；

②如图2，若CD在△AOB内部，请你在图2中画出完整图形，判断OM与AE之间的数量关系是否有变化？写出你的猜想，并加以证明；

③将△CDE绕点O任意转动，写出OM的取值范围（用含a式子表示）；

（2）是否存在边长最大的△AOB，使△CDE的三个顶点分别在△AOB的三条边上（都不与顶点重合）？如果存在，请你画出此时的图形，并求出边长a的值；如果不存在，请说明理由．

Answer 1

【答案】（1）①OM＝AE；②OM＝AE，证明详见解析；③≤OM≤；（2）存在，．

【解析】

（1）①利用△CDE≌△AOB得出BC＝AE，再由直角三角形斜边的中线等于斜边的一半求解．

②作辅助线，利用△COF≌△EOA及三角形中位线得出OM＝AE．

③分两种情况，当OC与OB重合时OM最大，当OC在BO的延长线上时OM最小，据此求出OM的取值范围．

（2）分两种情况：当顶点D在斜边AB上时，设点C，点E分别在OB，OA上．由DM+OM≥OF求出直角边a的最大值；当顶点D在直角边AO上时，点C，点E分别在OB，AB上时，利用△EHD≌△DOC，得出OD＝EH，在Rt△DHE中，运用勾股定理ED2＝DH2+EH2，得出方程，由△判定出a的最大值．

解：（1）①∵△CDE和△AOB是两个等腰直角三角形，

∴CD＝ED，AO＝B0，∠CDE＝∠AOB，

在△CDE和△AOB中，

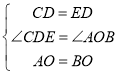
∴△CDE≌△AOB（SAS），

∴BC＝AE

∵M为BC中点，

∴OM＝BC，

∴OM＝AE．

②猜想：OM＝AE．

证明：如图2，延长BO到F，使OF＝OB，连接CF，

∵M为BC中点，

∴OM＝CF，

∵△CDE和△AOB是两个等腰直角三角形，

∴CD＝ED，AO＝BO＝OF，∠CDE＝∠AOB，

∵∠AOC+∠COB＝∠BOE+∠COB＝90°，

∴∠AOC＝∠BOE，

∠FOC＝∠AOE，

在△COF和△EOA中，

∴△COF≌△EOA，

∴CF＝AE，

∴OM＝AE．

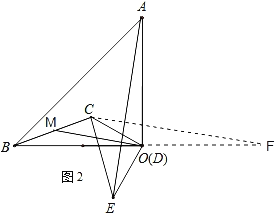
③Ⅰ、如图3，当OC与OB重合时，OM最大，

OM＝

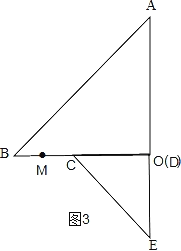
Ⅱ、如图4，当OC在BO的延长线上时，OM最小，

OM＝﹣1＝，

所以≤OM≤，

（2）解：根据△CDE的对称性，只需分两种情况：

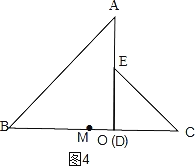
①如图5，

当顶点D在斜边AB上时，设点C，点E分别在OB，OA上． 作OF⊥AB于点F，取CE的中点M，连接OD，MD，OM．

∵△AOB和△CDE是等腰直角三角形，∠AOB＝∠CDE＝90°，OA＝OB＝a（a＞1），DC＝DE＝1，

∴AB＝a，OF＝AB＝a，

∴CE＝，DM＝CE＝，

在RT△COE中，OM＝CE＝，

在RT△DOM中，DM+OM≥OD，

又∵OD≥OF，

∵DM+OM≥OF，即+≥a，

∴a≤2，

∴直角边a的最大值为2．

②如图6，

当顶点D在直角边AO上时，点C，点E分别在OB，AB上，作EH⊥AO于点H．

∵∠AOB＝∠CDE＝∠DHE＝90°，

∵∠HED+∠EDH＝∠CDO+∠EDH＝90°，

∴∠HED＝∠CDO，

∵DC＝DE，

在△EHD和△DOC中，

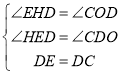
∴△EHD≌△DOC（AAS）

设OD＝x，

∴OD＝EH＝AH＝x，DH＝a﹣2x，

在Rt△DHE中，ED2＝DH2+EH2，

∴1＝x2+（a﹣2x）2，

整理得，5x2﹣4ax+a2﹣1＝0，

∵x是实数，

∴△＝（4a）2﹣4×5×（a2﹣1）＝20﹣4a2≥0，

∴a2≤5，

∴a2的最大值为5，

∴a的最大值为．

综上所述，a的最大值为．