题目内容
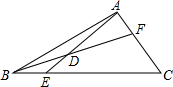
如图△ABC中，AF=FD=DH=HB，AG=GE=EK=KC，已知DE=6．求FG、BC、HK的长．
解：∵AF=FD=DH=HB，AG=GE=EK=KC，DE=6，
∴点D，E分别是AB，AC的中点，
∴BC=2DE=12，
同理：FG=3，
∵AF=FD=DH=HB，AG=GE=EK=KC，
∴AF：AH=1：3，AG：AK=1：3，
∴AG：HK=1：3，
∵FG=3，
∴HK=9．
∴点D，E分别是AB，AC的中点，
∴BC=2DE=12，
同理：FG=3，
∵AF=FD=DH=HB，AG=GE=EK=KC，
∴AF：AH=1：3，AG：AK=1：3，
∴AG：HK=1：3，
∵FG=3，
∴HK=9．
练习册系列答案
阅读快车系列答案
相关题目
已知：如图△ABC中，AF：FC=1：2，且BD=DF，那么BE：EC等于（ ）| A、1：4 | B、1：3 | C、2：5 | D、2：3 |
如图△ABC中，AF=FD=DH=HB，AG=GE=EK=KC，已知BC=12．求FG、DE、HK的长．
如图△ABC中，AF平分∠BAC交BC于F，FD⊥AB于D，FE⊥AC于E，求证：AF垂直平分DE．
如图△ABC中，AF=FD=DH=HB，AG=GE=EK=KC，已知DE=6．求FG、BC、HK的长．