Question

原点到直线y=

4

3

x+4的距离是

 

．

Answer 1

分析：在坐标系内画出函数图象，求出直线与坐标轴的交点坐标．
在直线与两坐标轴构成的直角三角形中求斜边上的高即是原点到直线的距离．

解答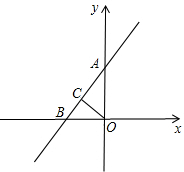：解：如图：
直线交x轴于B点，交y轴于A点，OC⊥AB于C点．
令x=0，则y=4； 令y=0，则x=-3．
∴OA=4，OB=3．
∴AB=

42+32

=5．
∵S_△AOB=

1

2

OA•OB=

1

2

AB•OC，
∴OC=

3×4

5

=

12

5

．
即原点到直线y=

4

3

x+4的距离是

12

5

．
故答案为

12

5

．

点评：此题考查一次函数及其图象的应用以及点到直线的距离等知识点，综合性强，难点大．