题目内容
（1）在Rt△ABC中，∠C=90°，∠A的正弦、余弦之间有什么关系？请给出证明过程．
（2）已知锐角α满足：sinα=1-x，cosα=1-2x，求tanα的值．
解：（1）∵Rt△ABC中，∠C=90°，
∴a2+b2=c2
∵sinA=
cosA=
∴sin2A+cos2A=（）2+（）2=
=
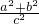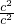=1
故sin2A+cos2A=1
（2）由sin2α+cos2α=1，得（1-x）2+（1-2x）2=1，
解得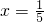
或x=1（舍）
∴tanα=
=
=
=
=
．
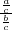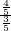分析：（1）利用正弦与余弦的定义及勾股定理得到同角的正弦与余弦之间的关系；
（2）利用上题证得的关系式代入求解即可．
点评：本题考查了同角的三角函数的关系，解题的关键是熟记各个锐角三角函数之间的关系．
∴a2+b2=c2
∵sinA=
cosA=∴sin2A+cos2A=（
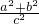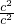）2+（）2===1故sin2A+cos2A=1
（2）由sin2α+cos2α=1，得（1-x）2+（1-2x）2=1，
解得
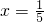或x=1（舍）∴tanα=
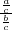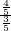====．分析：（1）利用正弦与余弦的定义及勾股定理得到同角的正弦与余弦之间的关系；
（2）利用上题证得的关系式代入求解即可．
点评：本题考查了同角的三角函数的关系，解题的关键是熟记各个锐角三角函数之间的关系．
练习册系列答案
相关题目
23、如图，在Rt△ABC中，∠ACB=90°，D、E是边AB上两点，且CE所在直线垂直平分线段AD，CD平分∠BCE，AC=5cm，求BD的长．