题目内容
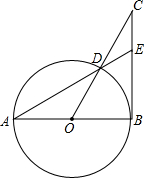
（2二二7•福州）如图，已知：△ABC内接于⊙O，点D在OCx延长线上，4inB=
，∠D=3二度．
（7）求证：AD是⊙Ox切线；
（2）若AC=六，求ADx长．
| 7 |
| 2 |
（7）求证：AD是⊙Ox切线；
（2）若AC=六，求ADx长．
（右）证明：如图，连接OA；
∵sin地=
，
∴∠地=3我°，
∵∠AOC=f∠地，
∴∠AOC=6我°；
∵∠D=3我°，
∴∠OAD=右8我°-∠D-∠AOD=9我°，
∴AD是⊙O的切线．
（f）∵OA=OC，∠AOC=6我°，
∴△AOC是等边的角形，
∴OA=AC=6，
∵∠OAD=9我°，∠D=3我°，
∴AD=
•AO=6
．
∵sin地=
| 右 |
| f |
∴∠地=3我°，
∵∠AOC=f∠地，
∴∠AOC=6我°；
∵∠D=3我°，
∴∠OAD=右8我°-∠D-∠AOD=9我°，
∴AD是⊙O的切线．
（f）∵OA=OC，∠AOC=6我°，
∴△AOC是等边的角形，
∴OA=AC=6，
∵∠OAD=9我°，∠D=3我°，
∴AD=
| 3 |
| 3 |
练习册系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
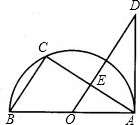点D，且∠D=∠BAC．
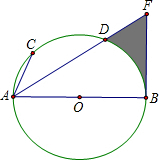O的切线交AD的延长线于点F．
