Question

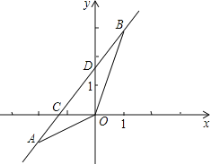
【题目】如图是某公园的一角，∠AOB=90°，弧AB的半径OA长是6m，C是OA的中点，点D在弧AB上，CD//OB，则图中休闲区（阴影部分）的面积是（ ）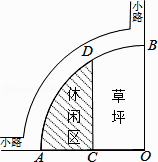
A.
B.
C.
D.

Answer 1

【答案】A
【解析】解：连接OD，
∵弧AB的半径OA长是6米，C是OA的中点，
∴OC= OA= ×6=3米，
∵∠AOB=90°，CD//OB，
∴CD⊥OA，
在Rt△OCD中，
∵OD=6，OC=3，
∴CD= = =3 米，
∵sin∠DOC= = = ，
∴∠DOC=60°，
∴S阴影=S扇形AOD﹣S△DOC= ﹣ ×3×3 =（6π﹣ ）平方米．
故选A．
【考点精析】根据题目的已知条件，利用平行线的性质和扇形面积计算公式的相关知识可以得到问题的答案，需要掌握两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补；在圆上，由两条半径和一段弧围成的图形叫做扇形；扇形面积S=π（R2-r2）．