题目内容
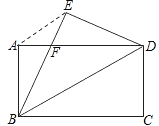
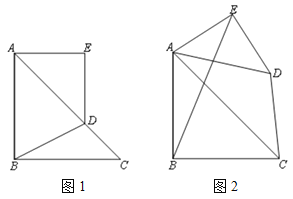
【题目】如图1,![]() 都是等腰直角三角形,
都是等腰直角三角形,![]() ,且
,且![]() ,点
,点![]() 在
在 ![]() 上,连接
上,连接![]() .
.
(1)如果![]() ,①求
,①求![]() ;②若
;②若![]() 是关于
是关于![]() 的方程
的方程![]() 的两个实数根,求
的两个实数根,求![]() 的值;
的值;
(2)如图2,将![]() 绕点
绕点![]() 逆时针旋转,使
逆时针旋转,使![]() ,连接
,连接![]() ,求五边形
,求五边形![]() 的面积.
的面积.
【答案】(1)①![]() ,②
,②![]() ;(2)五边形
;(2)五边形![]() 的面积为
的面积为![]() .
.
【解析】
(1)①延长ED交BC于点F,表示出DF、BF,然后利用勾股定理列出方程,再把c=![]() a代入求出a、b的关系即可;
a代入求出a、b的关系即可;
②利用根与系数的关系表示出a+b,ab,然后消掉a、b得到关于m的一元二次方程,然后求解即可;
(2)过A,C,D分别向BE作垂线,垂足分别为H,M,N,根据同角的余角相等求出∠HAE=∠NED,然后利用“角角边”证明△AHE和△END全等,同理可证△AHB≌BMC,根据全等三角形对应边相等可得AH=MB=EN,MC=BH,DN=EH,设AH=h,然后根据五边形的面积等于两对全等三角形的面积加上梯形的面积列式整理即可得解.
(1)①延长ED交BC于点F,
![]() ,
,
在![]() 中由勾股定理得,
中由勾股定理得, ![]() ,
,
又![]()
![]() ,
,
![]() 或
或![]() ,
,
又![]() ,
,
∴![]() ;
;
②由根与系数的关系![]() ,
,
由![]() ,
,
解得![]() ,
,
所以, ![]() ,
,
整理得, ![]() ,
,
解得![]() ,
,
![]() ,
,
![]() ,
,
当![]() 时,方程为
时,方程为![]() ,这个方程有两个不相等的正根,
,这个方程有两个不相等的正根,
所以,![]() 符合题意;
符合题意;
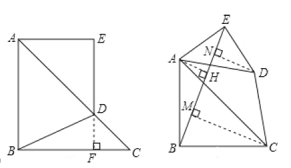
(2)过![]() 分别向
分别向![]() 作垂线,垂足分别为
作垂线,垂足分别为![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在![]() 与
与![]() 中,
中,
![]() ,
,
![]()
同理可证![]() ,
,
则![]() ,
,
设![]() ,
,
五边形![]() 的面积为
的面积为![]() .
.

练习册系列答案
相关题目