题目内容
5.如果一个多边形的内角和与外角和的差是1440°,那么这个多边形是几边形?分析 已知一个多边形的内角和与外角和的差为1440°,外角和是360°,因而内角和是1800°.n边形的内角和是(n-2)•180°,代入就得到一个关于n的方程,就可以解得边数n.
解答 解:根据题意,得
(n-2)•180=1800,
解得:n=12.
答:这个多边形是十二边形.
点评 本题主要考查多边形的外角和与内角和,熟练掌握n边形内角和为(n-2)•180°、外角和为360°是解题的关键.

练习册系列答案
相关题目
17.下列图标中,既是中心对称图形又是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
17.某市为了方便广大群众绿色出行,在城市设置了若干个站点,进行公共自行车租赁服务,并实行累加计费,具体计费标准如下:
(例如:使用者用车5小时,则系统收费:0+1+2+3+3=9元)
(1)九年级同学集体出游,若租赁自行车的时间是7个小时(每人一辆),其他花费是300元,请写出这次出游的总费用y(元)和学生人数x(名)之间的关系式;
(2)由于一名同学临时有事,仅仅租了两个小时就归还了自行车,这次出游的总费用是886元,请问共有多少名同学(包括这名有事的同学在内)参加了这次出游?
| 租赁时间<1小时 | 免费 |
| 1小时<租赁时间≤2小时 | 1元 |
| 2小时<租赁时间≤3小时 | 2元 |
| 租赁时间>3小时 | 3元/小时(不足1小时按1小时计) |
| 租赁时间≤24小时 | 最高收费30元 |
(1)九年级同学集体出游,若租赁自行车的时间是7个小时(每人一辆),其他花费是300元,请写出这次出游的总费用y(元)和学生人数x(名)之间的关系式;
(2)由于一名同学临时有事,仅仅租了两个小时就归还了自行车,这次出游的总费用是886元,请问共有多少名同学(包括这名有事的同学在内)参加了这次出游?
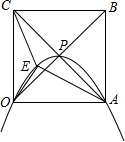 正方形OABC的边长为4,对角线相交于点P,抛物线L经过O、P、A三点,点E是正方形内的抛物线上的动点.
正方形OABC的边长为4,对角线相交于点P,抛物线L经过O、P、A三点,点E是正方形内的抛物线上的动点.