题目内容
11. 如图,已知在正方形ABCD中,点O为对角线AC的中点,过O点的射线OM、ON分别交AB、BC于点E、F,且∠EOF=90°,BO、EF交于点P,则下面结论中:
如图,已知在正方形ABCD中,点O为对角线AC的中点,过O点的射线OM、ON分别交AB、BC于点E、F,且∠EOF=90°,BO、EF交于点P,则下面结论中:①图形中全等的三角形只有三对;②△EOF是等腰直角三角形;
③正方形ABCD的面积等于四边形OEBF面积的4倍;
④BE+BF=$\sqrt{2}$OA;⑤AE2+BE2=2OP•OB.
正确结论的个数是( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 由正方形的性质和已知条件得出图形中全等的三角形有四对,得出①不正确;
由△AOE≌△BOF,得出对应边相等OE=OF,得出②正确;
由△AOE≌△BOF,得出四边形OEBF的面积=△ABO的面积=$\frac{1}{4}$正方形ABCD的面积,③正确;
由△BOE≌△COF,得出BE=CF,得出BE+BF=AB=$\sqrt{2}$OA,④正确;
由△AOE≌△BOF,得出AE=BF,得出AE2+CF2=BE2+BF2=EF2=2OF2,再证明△OPF∽△OFB,得出对应边成比例OP:OF=OF:OB,得出OF2=OP•OB,得出⑤正确.
解答 解:①不正确;
图形中全等的三角形有四对:△ABC≌△ADC,△AOB≌△COB,△AOE≌△BOF,△BOE≌△COF;理由如下:
∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠BAD=∠ABC=∠BCD=∠D=90°,∠BAO=∠BCO=45°,
在△ABC和△ADC中,$\left\{\begin{array}{l}{AB=AD}&{\;}\\{BC=DC}&{\;}\\{AC=AC}&{\;}\end{array}\right.$,
∴△ABC≌△ADC(SSS);
∵点O为对角线AC的中点,
∴OA=OC,
在△AOB和△COB中,$\left\{\begin{array}{l}{OA=OC}&{\;}\\{AB=CB}&{\;}\\{OB=OB}&{\;}\end{array}\right.$,
∴△AOB≌△COB(SSS);
∵AB=CB,OA=OC,∠ABC=90°,
∴∠AOB=90°,∠OBC=45°,
又∵∠EOF=90°,
∴∠AOE=∠BOF,
在△AOE和△BOF中,$\left\{\begin{array}{l}{∠OAE=∠OBF=45°}&{\;}\\{OA=OB}&{\;}\\{∠AOE=∠BOF}&{\;}\end{array}\right.$,
∴△AOE≌△BOF(ASA);
同理:△BOE≌△COF;
②正确;理由如下:
∵△AOE≌△BOF,
∴OE=OF,
∴△EOF是等腰直角三角形;
③正确.理由如下:
∵△AOE≌△BOF,
∴四边形OEBF的面积=△ABO的面积=$\frac{1}{4}$正方形ABCD的面积;
④正确.理由如下:
∵△BOE≌△COF,
∴BE=CF,
∴BE+BF=CF+BF=BC=AB=$\sqrt{2}$OA;
⑤正确.理由如下:
∵△AOE≌△BOF,
∴AE=BF,
∴AE2+CF2=BE2+BF2=EF2=2OF2,
在△OPF与△OFB中,
∠OBF=∠OFP=45°,
∠POF=∠FOB,
∴△OPF∽△OFB,
∴OP:OF=OF:OB,
∴OF2=OP•OB,
∴AE2+CF2=20P•OB.
正确结论的个数有4个;
故选:A.
点评 本题是四边形综合题目,考查了全等三角形的判定与性质、正方形的性质、等腰直角三角形的判定与性质、相似三角形的判定与性质等知识;本题难度较大,综合性强,需要证明三角形全等和三角形相似才能得出结论.

| A. | 明天某地区早晨有雾 | |
| B. | 抛掷一枚质地均匀的骰子,向上一面的点数是6 | |
| C. | 一个不透明的袋子中有2个红球和1个白球,从中摸出1个球,该球是黑球 | |
| D. | 明天见到的第一辆公交车的牌照的末位数字将是偶数 |
 如图,已知BE是△ABC的外接圆的直径,CD⊥AB于D,若AD=3,BD=8,CD=6,则BE的长为5$\sqrt{5}$.
如图,已知BE是△ABC的外接圆的直径,CD⊥AB于D,若AD=3,BD=8,CD=6,则BE的长为5$\sqrt{5}$.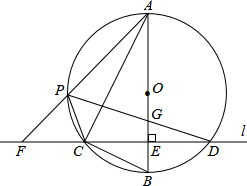 如图,在⊙O的内接△ABC中,∠ACB=90°,tan∠CAB=$\frac{1}{2}$,过C作AB的垂线l交⊙O于另一点D,垂足为E.设P是$\widehat{AC}$上异于A,C的一个动点,射线AP交l于点F,连接PC与PD,PD交AB于点G.
如图,在⊙O的内接△ABC中,∠ACB=90°,tan∠CAB=$\frac{1}{2}$,过C作AB的垂线l交⊙O于另一点D,垂足为E.设P是$\widehat{AC}$上异于A,C的一个动点,射线AP交l于点F,连接PC与PD,PD交AB于点G.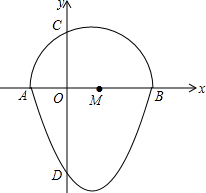 我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图,点A、B、C、D分别是“蛋圆”与坐标轴的交点,AB为半圆的直径,点M为圆心,A点坐标为(-2,0),B点坐标为(4,0),D点的坐标为(0,-4).
我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图,点A、B、C、D分别是“蛋圆”与坐标轴的交点,AB为半圆的直径,点M为圆心,A点坐标为(-2,0),B点坐标为(4,0),D点的坐标为(0,-4).