题目内容
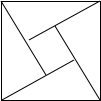 第二十四届国际数学家大会在北京举行,其会标如图所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.
第二十四届国际数学家大会在北京举行,其会标如图所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.(1)试说明大正方形与小正方形是否相似;
(2)若大方形的面积为13,每个直角三角形两直角边的和为5,求大正方形与小正方形的相似比.
考点:相似多边形的性质
专题:
分析:(1)如果两个多边形的对应角相等,对应边的比相等,则这两个多边形是相似多边形.依此定义即可判定大正方形与小正方形相似;
(2)设直角三角形的直角边中长边为a,短边为b,根据大正方形面积为13和a+b=5列出方程组,解方程组即可解题.
(2)设直角三角形的直角边中长边为a,短边为b,根据大正方形面积为13和a+b=5列出方程组,解方程组即可解题.
解答:解:(1)∵正方形的四条边都相等,四个角都是直角,
∴大正方形与小正方形的对应角相等,对应边的比相等,
∴大正方形与小正方形相似;
(2)设直角三角形的长直角边为a,短直角边为b,
由题意,得
,
解得
.
∵大方形的边长为
,小方形的边长为a-b=3-2=1,
∴大正方形与小正方形的相似比为
:1=
.
∴大正方形与小正方形的对应角相等,对应边的比相等,
∴大正方形与小正方形相似;
(2)设直角三角形的长直角边为a,短直角边为b,
由题意,得
|
解得
|
∵大方形的边长为
| 13 |
∴大正方形与小正方形的相似比为
| 13 |
| 13 |
点评:本题考查了相似多边形的定义,勾股定理在直角三角形中的灵活应用,正方形各边长相等的性质,难度适中.

练习册系列答案
相关题目
若x-y≠0,2x-3y=0,则分式
的值是( )
| 10x-11y |
| x-y |
| A、-12 | ||
| B、0 | ||
| C、8 | ||
D、8
|
若分式
的值为0,则x的值为( )
| x2-4 |
| x-2 |
| A、±2 | B、-2 | C、0 | D、2 |
